Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 49

Considere X o número de vezes que certa máquina de controle numérico irá funcionar de maneira errada: uma, duas ou três vezes em qualquer dia. Seja Y o número de vezes que o técnico é chamado para uma emergência. Suas distribuições de probabilidade conjuntas são

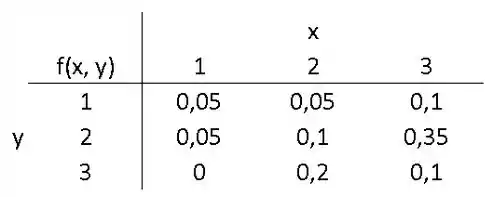
(a) Avalie a distribuição marginal de X.

(b) Avalie a distribuição marginal de Y

(c) Determine P   ( Y = 3 | X = 2 ) .

Passo 1

Falaa, meu querido/minha querida. Como X e Y são variáveis aleatórias discretas. A função de massa de probabilidade conjunta p ( x ,   y ) é:

p x ,   y = P ( X = x ,   Y = y )

Para todos os pares ( x ,   y ) , onde p x ,   y ≥ 0 e ∑ x ∑ y p x ,   y = 1 .

Então, bora realizar a questão!!!

Passo 2

Para encontrarmos a distribuição marginal de x precisamos usar a tabela do enunciado.

Quando x = 1 :

f X x = ∑ y p x , y = p 1 ,   1 + p 1 ,   2 + p 1 ,   3

= 0,05 + 0,05 + 0 = 0,1

Para x = 2 :

f X x = ∑ y p x , y = p 2 ,   1 + p 2 ,   2 + p 2 ,   3

= 0,0 5 + 0 , 1 + 0 , 2 = 0 , 35

Para x = 3 :

f X x = ∑ y p x , y = p 3 ,   1 + p 3 ,   2 + p 3 ,   3

= 0,05 + 0 , 35 + 0 , 1 = 0 , 55

Logo, distribuição de probabilidade marginal de x é:

Passo 3

De forma similar a letra (a).

Quando y = 1 :

f Y y = ∑ x p x , y = p 1 ,   1 + p 2 ,   1 + p 3 ,   1

= 0,05 + 0,05 + 0 , 1 = 0 , 2

Para y = 2 :

f Y y = ∑ x p x , y = p 1 ,   2 + p 2 ,   2 + p 3 ,   2

= 0,05 + 0 , 1 + 0 , 35 = 0 , 5

Para y = 1 :

f Y y = ∑ x p x , y = p 1 ,   3 + p 2 ,   3 + p 3 ,   3

= 0 + 0 , 2 + 0 , 1 = 0 , 3

Logo, distribuição de probabilidade marginal de y é:

Passo 4

A probabilidade do evento { Y = 3 | X = 2 } é dada por:

P Y = 3 X = 2 = f Y | X 3 2 = f ( 2 ,   3 ) f X ( 2 )

= 0,2 0,35

P Y = 3 X = 2 = 0,57

Os dois valores podem ser encontrados na letra (a).

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Na estimativa de custo, o preço total de um projeto é a soma dos gastos das tarefas componentes. Cada custo é uma variável aleatória com uma distribuição de probabilidade. É costume obter informações
Um restaurante serve três pratos ao preço fixo de US$ 12, US$ 15 e US$ 20. Para um casal selecionado aleatoriamente que janta nesse restaurante, sejam X custo do jantar do homem e Y custo do jantar da
Sejam A a porcentagem de um elemento de um espécime de rocha selecionado aleatoriamente, e B a porcentagem de um segundo elemento desse mesmo espécime. Suponha que D e E sejam erros de medição ao dete
Um espécime de rocha de uma área específica é selecionado aleatoriamente e pesado duas vezes. Represente por W o peso real e por X 1 e X 2 os dois pesos medidos. Então, X 1 = W + E 1 e X 2 = W + E 2 ,
Sejam X 1 , … , X n vas independentes com valores médios μ 1 , … , μ n e variâncias σ 1 2 , … , σ n 2 . Considere uma função h x 1 , … , x n e use-a para definir uma nova va Y = h X 1 , … , X n . Sob