Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 82

82. Considere as 10 observações a seguir de vida útil de mancais (em horas):

152,7 172,0 172,5 173,3 193,0 204,7 216,5 234,9 262,6 422,6

Construa o gráfico de probabilidade normal e comente sobre a plausibilidade da distribuição normal como modelo de estimativa da vida útil de mancais (dados obtidos em “Modified Moment Estimation for the Three-Parameter Lognormal Distribution,” J. Quality Technology, 1985, p. 92 -99).

Passo 1

Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.

Dados construídos em percentil pelas observações:

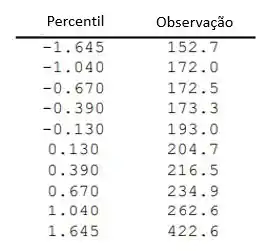
Gráfico de probabilidade normal:

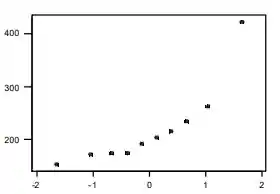
O gráfico é bastante reto, exceto pelo ponto correspondente à maior observação. Esta observação é claramente muito maior do que seria esperado em uma amostra aleatória normal. Por causa desse outlier, seria desaconselhável analisar os dados usando qualquer método inferencial que dependesse de assumir uma distribuição populacional normal.

Até a próxima, pessoal!

Resposta

No passo 1.

Exercícios de Livros Relacionados

Seja X uma variável aleatória com a seguinte distribuição de probabilidade:Determine o desvio padrão de X .
No Exercício 3.31, a distribuição do tempo antes de um reparo considerável em uma máquina de lavar era dada por f y = { 1 4 e - y 4 , y ≥ 00 , c a s oc o n t r á r i o á Qual é a média populacional do
A variável aleatória X , que representa o número de erros por cem linhas de um código de software, tem a seguinte distribuição de probabilidade:Usando o teorema 4.2, determine a variância de X .
A proporção de pessoas que respondem a certa solicitação de compras por catálogo é a variável aleatória X , tendo a função de densidade dada no Exercício 4.14. Determine a variância deX .
O lucro de um revendedor, em unidades de $5.000 , com um novo automóvel, é a variável aleatória X que tem a função de densidade dada no Exercício 4.12. Determine a variância deX .