Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 46
Construa um conjunto de dados pareados para o qual t , de modo que os dados sejam altamente significativos quando a análise correta é usada, ainda que t para o teste t de duas amostras esteja bem próximo de zero, assim, a análise incorreta produz um resultado insignificante.
Passo 1
O teste t emparelhado:
Quando (diferença entre observações dentro de um par), e hipótese nula
o valor da estatística de teste para testar as hipóteses é
onde são a média amostral e o desvio padrão amostral das diferenças , respectivamente. Para usar este teste, suponha que as diferenças são de uma população normal. Dependendo da hipótese alternativa, o valor de PP pode ser determinado como a área correspondente sob curva a
O objetivo aqui é encontrar um conjunto de dados para o qual t seja infinito. A partir de
t é infinito quando é zero
Passo 2
A variância da amostra é
Onde
O desvio padrão da amostra s é
A partir da definição, é zero se e somente se
para cada Isso agora indica que todos os dados devem ser iguais. NOTA: os dados para as diferenças devem ser iguais, não o conjunto de dados emparelhado
A partir desta conclusão, vamos assumir que a diferença é por exemplo 0,5, o conjunto de dados escolhido é dado na tabela abaixo (tomando números para os quais .
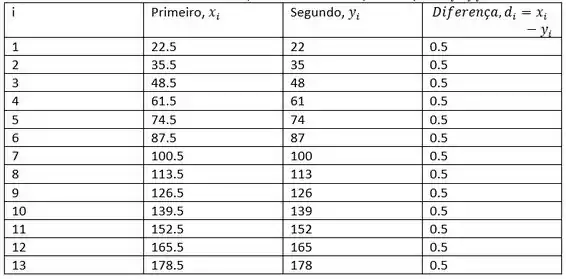
Obviamente, para o teste t pareado t=0, porque o desvio padrão da amostra para as diferenças é
Então
Vamos ver o que acontece com t para o teste t de duas amostras.
O teste t de duas amostras para teste
usa o seguinte valor da estatística de teste
Para a hipótese alternativa adequada a área adequada sob o curva é o valor de P.
a média amostral do primeiro conjunto de dados é
e o desvio padrão da amostra é
E
Passo 3
só há diferença na média amostral de 0.5 porque o conjunto de dados foi escolhido assim, porém calcule a média amostral do segundo conjunto de dados
e o desvio padrão da amostra é
E
O valor estatístico do teste de teste t de duas amostras é
que é quase zero.
A análise incorreta produz um resultado insignificante.
Resposta
A análise incorreta produz um resultado insignificante.