Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 38
Espécimes de concreto com razões de altura/diâmetro variáveis cortados em várias posições no cilindro original foram obtidos de uma mistura de concreto de resistência normal e de uma mistura de alta resistência tensão de pico (MPa) foi determinada para cada mistura, resultando nos dados a seguir ("Effect of Length on Compressive Strain Softening of Concrete," J. of Engr. Mechanics, 1997, p. 25-35):
a. Construa um boxplot comparativo das tensões de pico para os dois tipos de concreto e comente sobre quaisquer características interessantes. b. Calcule a diferença entre as tensões de pico médias reais dos dois tipos de concreto, de forma que forneça informações sobre precisão e confiabilidade. Certifique-se de verificar a plausibilidade de quaisquer hipóteses necessárias em sua análise. Parece plausível que as tensões de pico médias reais dos dois tipos de concreto sejam idênticas? Por que sim ou por que não?
Passo 1
- Para desenhar um boxplot, precisamos encontrar a mediana, quartil superior e inferior, "bigodes" superior e inferior e eventuais outliers.
Demonstraremos o procedimento para encontrar esses valores apenas para o conjunto de dados "Alto".
Seja sejam as observações no conjunto de dados "Alto". Como o tamanho da amostra é n=15, então a mediana da amostra é
O quartil superior é
O quartil inferior é
Portanto, o intervalo interquartil é
O "bigode" inferior é o menor valor amostral não inferior a
que neste caso é , que é o menor valor da amostra.
Passo 2
O "bigode" superior é o maior valor amostral não maior que
que neste caso é , que é o maior valor da amostra.
Os valores atípicos são todos os valores de amostra menores que o "bigode" inferior ou maiores que o "bigode" superior, e podemos descobrir que não há valores atípicos nesta amostra.
Agora, os lados horizontais da caixa mostram o quartil superior e inferior, a linha em negrito dentro da caixa marca o valor mediano e as linhas que se estendem da caixa atingem os "bigodes" superior e inferior. Outliers são mostrados como pequenos círculos (não presentes aqui).
As quantidades necessárias para o conjunto de dados "Normal" são
Os valores 55,4 e 55,6 são valores discrepantes.
Os boxplots são mostrados na imagem abaixo.
Podemos ver que o boxplot para o pico de tensão de uma mistura de concreto de alta resistência está posicionado bem acima do boxplot para o pico de tensão de uma mistura de resistência normal.
Isso nos mostra que o pico de tensão tende a ser muito maior para a mistura de alta resistência do que para a mistura de resistência normal.
Aqui está a imagem:
Temos que n=15 é o número de pares em nossa amostra, e que são variáveis aleatórias independentes e identicamente distribuídas com média e desvio padrão , ambos desconhecidos (estes representam o pico de tensão de uma mistura de concreto de alta resistência).
Cada tem seu valor emparelhado , então são variáveis aleatórias independentes e identicamente distribuídas com média e desvio padrão , ambos desconhecidos (estes representam o pico de tensão de uma mistura de concreto de resistência normal).
Devemos encontrar um intervalo de confiança para a verdadeira diferença nas médias populacionais , pois pode fornecer as informações solicitadas sobre a precisão de nossa estimativa.
O nível de confiança não é fornecido, então vamos encontrar um intervalo de confiança de 99% para .
Lembre-se de que um intervalo de confiança para , é da forma
onde é a média amostral das diferenças pareadas (que são calculadas como para todo ) e é o desvio padrão da amostra daqueles.
Passo 2
Este intervalo de confiança é válido se a distribuição das diferenças for aproximadamente normal, então precisamos verificar isso primeiro. Para fazer isso, vamos desenhar o gráfico de probabilidade normal.
Antes disso, precisamos calcular as diferenças emparelhadas. Agora fornecemos a tabela de medidas e as diferenças pareadas calculadas:
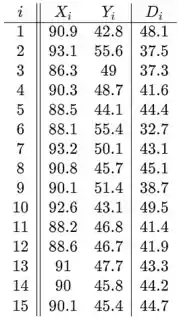
Agora, o gráfico de probabilidade normal traça as observações ordenadas (diferenças) versus os quantis normais, que são na verdade valores , para todo , onde é a função de distribuição cumulativa de uma variável aleatória normal padrão, e é sua função inversa.
Usamos o software estatístico R para desenhar o gráfico de probabilidade normal. Por exemplo, o comando
qqnorm(x)
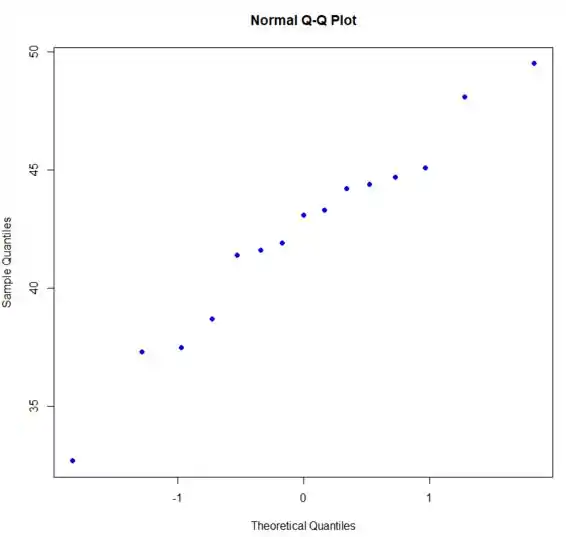
irá desenhar o gráfico desejado, que é mostrado na imagem abaixo.
A trama mostra retidão, e o desvio que existe não parece ser grande o suficiente para podermos rejeitar a hipótese de normalidade.
Em outras palavras, podemos supor que nossas diferenças pareadas são aproximadamente normalmente distribuídas.
Aqui está o gráfico:
Podemos descobrir que a média amostral das diferenças pareadas é
e o desvio padrão da amostra das diferenças pareadas é
A única coisa que resta a encontrar é o quantil (o número dos graus de liberdade é ), e podemos encontrá-lo usando a Tabela A.5 nas Tabelas do Apêndice.
Encontramos a linha rotulada com (esses são os graus de liberdade) e a coluna rotulada com (porque , então =0.005), e a quantidade desejada está localizada no corpo da tabela, sob essa linha e coluna, e podemos descobrir que é .
Finalmente, substituindo todos os valores, na fórmula para o intervalo de confiança de fornecido acima, nos dá o intervalo de confiança de desejado para :
Esse intervalo nos mostra que podemos ter de certeza de que a tensão de pico média real de uma mistura de concreto de alta resistência é entre 38.77 MPa e 45.68 MPa maior do que a de uma mistura de concreto de resistência normal.
Podemos, portanto, estar altamente confiantes de que as tensões de pico médias para os dois tipos de concreto não são iguais (o intervalo de confiança está muito acima do valor de 0).
Resposta
- O resumo de cinco números para o conjunto de dados "Alto" é , e para o conjunto de dados "Normal" é ;
- O intervalo de confiança de 99% para a diferença em duas médias populacionais é e está muito acima do valor de 0, então as duas médias quase certamente não são iguais