Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.2 - Ex. 4b
O consumo médio de gasolina num certo tipo de automóvel é de , segundo informações da montadora. Uma revista especializada verificou o consumo de 25 desses veículos, escolhidos ao acaso, e constatou consumo médio de . Admita que o consumo siga no modelo Normal com variância igual a .
- Determine a probabilidade de erro tipo .
Passo 1
Novamente, como na alternativa A, temos:
.
E
Do enunciado temos:
Da letra A, nosso teste era o seguinte:
Passo 2
Dessa vez, queremos a probabilidade de Erro tipo .
Lembrando que esse erro representa a chance de aceitarmos uma vez que essa hipótese é falsa. Em outras palavras:
Lembrando que definimos nossa RC da seguinte forma:
Usando aquela aproximação citada antes, isolando :
Portanto, se nossa média for menor do que então rejeitaremos .
Passo 3
Portanto, para o erro :
Teremos:
Agora, precisamos buscar na tabela de distribuição normal, , sabendo que:
Então, na tabela:
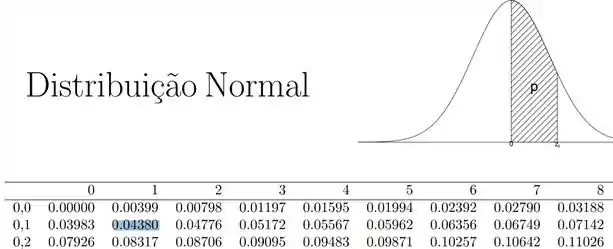
E podemos concluir:
Resposta
Concluindo, a probabilidade de aceitarmos a hipótese nula quando ela for falsa é de .