Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 6.Exercícios - Ex. 1
Dada uma distribuição normal padrão, determine a área abaixo da curva que fica
(a) à esquerda de ;
(b) à direita de
(c) entre
(d) à esquerda de
(e) à direita de ;
(f) entre
Passo 1
Vamos resolver um exercício de probabilidade juntos?
Nosso exercício é bem teórico sobre distribuição normal padrão, então vamos com calma para fixarmos bem a teoria.
A nossa Tabela-A3 pertencente ao livro do Walpole, nos dá
Ou seja, dado um qual a probabilidade de ele ser menor que determinado
Desenhando, seria algo do tipo:
Para :
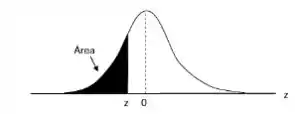
Para :
Com isso em mente, vamos resolver os itens enunciados.
Passo 2
Comecemos pelo princípio, pelo item a)
Queremos a área abaixo da curva que fica à esquerda de .
OPA! A nossa tabela nos dá exatamente a área a esquerda de um determinado, logo só precisamos encontrar este valor tabelado.
Para encontrá-lo, prosseguimos da seguinte maneira:
Na primeira coluna a esquerda da tabela, fixamos 1,4 (que são os dois primeiros dígitos que estamos trabalhando) e andamos em linha até 0,03, para formarmos o número 1,43.
Desse modo, obtemos:
Show, de acordo com a nossa tabela, a área à esquerda de é numericamente igual a .
Vamos ao item b)
Neste item queremos a área a direita de
De maneira clara, nós obteremos um valor na tabela para e este será numericamente igual a área A ESQUERDA DE , para encontrarmos a área a direita usaremos o seguinte fato
Logo,
Agora ficou fácil, só encontrar o valor tabelado para , encontrando, temos:
Show, este é o valor que encontramos para a área à direita de .
Agora vamos ao item c)
Nesse item estamos procurando a área entre
Em suma, queremos:
Fazendo essa manipulação ficamos com o intervalo desejado em mãos, e com os dois valores tabelados.
Assim, substituindo os valores encontrados na tabela:
Passo 3
Show! A partir daqui, partiremos para o item d.
Queremos a área à esquerda de ; e como sabemos, a nossa tabela sempre fornece os valores da área à esquerda de determinado .
Assim, encontrando o valor tabelado, temos: que é o valor da área que queremos.
Partiremos ao item e) agora.
Queremos nesse item a área à direita de
Usaremos o mesmo truque do item b)
Logo,
Traduzindo essa equação para o português claro: A área à direita de é igual a área total da distribuição menos a área à esquerda de .
A área a esquerda é um valor tabelado, logo ficamos com:
Que é o valor da área que queremos.
Por fim, vamos ao item f), onde é pedido a área entre
Usaremos o mesmo truque usado no item c)
Agora temos dois valores tabelados, substituindo os valores encontrados na tabela:
Que é o valor da área que queremos.
Resposta
a)
b)
c)
d)
e)
f)