Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 3

Um determinado mercado tem uma fila de caixa expressa e uma fila de caixa superexpressa. Represente por X 1 o número de clientes na fila da caixa expressa em um determinado horário do dia e por X 2 o número de clientes na fila da caixa superexpressa no mesmo horário. Suponha que a fmp conjunta de X 1 e X 2 seja dada na tabela a seguir.

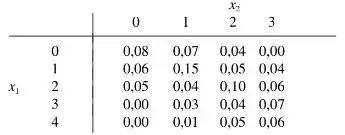
a. Qual é P ( X 1 = 1 ,   X 2 = 1 ), isto é, a probabilidade de haver exatamente um cliente em cada fila?

b. Qual é P ( X 1 = X 2 ) , isto é, a probabilidade de os números de clientes nas duas filas serem iguais?

c. Represente por A o evento de haver no mínimo dois clientes a mais em uma fila do que na outra. Expresse A em termos de X 1 e X 2 , e calcule a probabilidade desse evento.

d. Qual é a probabilidade de o número total de clientes nas duas filas ser exatamente quatro? E no mínimo quatro?

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Para resolvermos este exercício, precisamos apenas distribuir as probabilidades em p ( x , y ) e olharmos os valores correspondentes na tabela. Bora lá!!

Passo 2

A probabilidade pode ser analisada na tabela como primeira linha e primeira coluna. Sendo:

P X 1 = 1 ,   X 2 = 1 = p 1 ,   1 = 0,15

Passo 3

De novo usando a tabela para achar a probabilidade.

P X 1 = X 2 = p 0 ,   0 + p 1 ,   1 + p 2 ,   2 + p ( 3 ,   3 )

= 0,08 + 0,15 + 0,1 + 0,7

= 0,4

Passo 4

Podemos escrever o evento do enunciado como dois eventos:

X 1 ≥ 2 + X 2 e X 2 ≥ 2 + X 1

Logo, nós temos que:

A = X 1 ≥ 2 + X 2 ∪ X 2 ≥ 2 + X 1

O evento A pode ser representado na união de 9 eventos separados.

X 1 = x 1 , X 2 = x 1

Assim, podemos calcular a probabilidade.

P A = P X 1 ≥ 2 + X 2 ∪ X 2 ≥ 2 + X 1

= p 2 ,   0 + p 3 ,   0 + p 4 ,   0 + p 3 ,   1 + p 4 ,   1 + p 4 ,   2 + p 0 ,   2 + p 0 ,   3 + p 1 ,   3

= 0,05 + 0 + 0 + 0,03 + 0,01 + 0,05 + 0,04 + 0,04

= 0,22

Passo 5

Calculando a probabilidade de o número total de clientes nas duas filas ser quatro.

P X 1 + X 2 = 4 = p 1 ,   3 + p 2 ,   2 + p 3 ,   1 + p ( 4 ,   0 )

= 0,04 + 0,1 + 0,03 + 0

= 0,17

Calculando a probabilidade de ser no mínimo quatro clientes.

P X 1 + X 2 ≥ 4 = p 1 ,   3 + p 2 ,   2 + p 3 ,   1 + p 4 ,   0 + p 4 ,   1 + p 4 ,   2 + p 4 ,   3 + p 3 ,   2 + p 3 ,   3 + p ( 2 ,   3 )

= 0,46

Resposta

  1. P X 1 = 1 ,     X 2 = 1 = 0,15

  2. P X 1 = X 2 = 0 , 4 .

  3. P A = 0 , 22 .

  4. P X 1 + X 2 = 4 = 0 , 17 e P X 1 + X 2 ≥ 4 = 0,46 .

Exercícios de Livros Relacionados

Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjunta.Determine o seguinte: P ( X2.5 ,Y3 ) P(X P ( Y3 ) P ( X . 1.8 ,Y4.7 ) E ( X ) ,E ( Y ) ,V ( X )eV ( Y ) a
Quatro impressoras eletrônicas são selecionadas, provenientes de um grande lote de impressoras danificadas. Cada impressora é inspecionada e classificada como contendo um grande e um pequeno defeito.
Um artigo no Journal of Database Management “Experimental Study of a Self-Tuning Algorithm for DBMS Buffer Pools“ [“Estudo Experimental de um Algoritmo de Autoajuste para DBMS Buffer Pools “(2005. Vol
Uma fábrica usar dois dispositivos de inspeção para mostrar uma fração de sua saída, com objetivo de controlar a qualidade. O primeiro monitor de inspeção é capaz de detectar a cura da mente 99,3% dos
Uma classe de estatística para engenheiros tem 40 estudante, 60% de gente elétrica, 10% de engenharia industrial e 30% de engenharia mecânica. Uma amostra de quatro estudantes ser selecionado aleatori