Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 7

A distribuição de probabilidades conjuntas do número X   de carros e do número Y de ônibus por ciclo de semáforo em uma conversão à esquerda proposta é exibida na tabela de probabilidade conjunta a seguir.

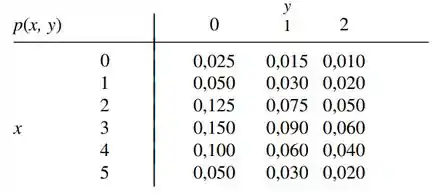
a. Qual é a probabilidade de haver exatamente um carro e exatamente um ônibus em um ciclo?

b. Qual é a probabilidade de haver no máximo um carro e no máximo um ônibus em um ciclo?

c. Qual é a probabilidade de haver exatamente um carro em um ciclo? E exatamente um ônibus?

d. Suponha que uma pista de conversão à esquerda tenha capacidade para cinco carros e um ônibus, equivalente a três carros. Qual é a probabilidade de excesso de fluxo em um ciclo?

e. X e Y são vas independentes? Explique.

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Para resolvermos essa questão, precisamos usar a fórmula abaixo:

p x ,   y = P ( X = x ,   Y = y )

Para todo par de x , y , onde p x ,   y ≥ 0 e ∑ x ∑ y p x , y = 1 .

De resto, vamos precisar apenas da tabela. Bora lá!!!

Passo 2

Pela tabela, achamos os seguintes valores:

P X = 1 , Y = 1 = p 1,1 = 0,3

Passo 3

Seguindo a mesma lógica:

P X ≤ 1   e   Y ≤ 1 = p 0 ,   0 + p 0 ,   1 + p 1 ,   0 + p ( 1 ,   1 )

= 0,025 + 0,015 + 0,05 + 0,03

= 0,12

Passo 4

A primeira probabilidade pedida:

P X = 1 = p 1 ,   0 + p 1 ,   1 + p ( 1 ,   2 )

= 0,05 + 0,03 + 0,2

= 0,1

A segunda probabilidade:

P Y = 1 = p 0 ,   1 + p 1 ,   1 + p 2 ,   1 + p 3 ,   1 + p 4 ,   1 + p ( 5 ,   1 )

= 0,3

Passo 5

O evento descrito pode ser escrito como a seguinte inequação:

X + 3 Y > 5

Portanto, calculando essa probabilidade:

P X + 3 Y > 5 = 1 - P ( X + 3 Y ≤ 5 )

= 1 - [ p 0 ,   0 + p 1 ,   0 + p 2 ,   0 + p 3 ,   0 + p 4 ,   0 + p 5 ,   0 + p 0 ,   1 + p 1 ,   1 + p 2 ,   1 ]

= 0,38

Passo 6

Por fim, para sabermos as variáveis são independentes elas devem respeitar a seguinte relação:

p x ,   y = p X ( x ) ∙ p Y ( y )

Para x = 1 e y = 1 , temos p X x = 0,1 e p Y y = 0,3 . Logo,

p 3 ,   3 = 0,3 ∙ 0,1

Pela tabela, vemos que a equação é verificada. Portanto, as variáveis são independentes.

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

O tempo entre os problemas de acabamento de uma superfície em um processo geral de galvanização é exponencialmente distribuído, com uma média de 40 horas. Uma única planta opera três linhas de galvani
Para a marca de referência do Conselho de desempenho do processamento de transação do exercício 5.10, sejam X, Y e Z e o número médio de operações de seleciona, atualizar e insere requerido para cada
A distribuição de probabilidades condicionais de Y, dado que ir a distribuição de probabilidade imaginar a justiça é uma distribuição contínuo uniforme de 0 a 10. Plote para vários valor de X. Determi
Dois método de medir a suavedade de uma superfície são usados para avaliar um produto feito de papel. As medidas, em unidade codificadas, são registradas como desvios em relação a um valor nominal da
Determine o valor de ser que torna a função uma função densidade de probabilidade conjunta ao longo da faixaDetermine o seguinte: