Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 45

Determine a covariância das variáveis aleatórias X e Y do Exercício 3.39.

Passo 1

Falaa, meu querido/minha querida. No Exercício 3.49, nos foi dada a seguinte distribuição de probabilidade conjunta para as variáveis X e Y :

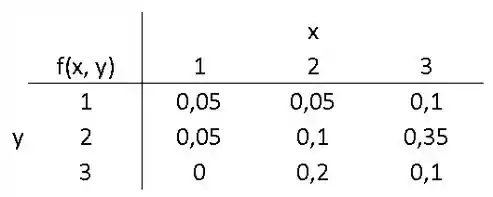
E a covariância nós vamos encontrar pela fórmula abaixo:

σ X Y = ∑ x ∑ y x - μ X y - μ Y f ( x , y )

Então, bora para os cálculos!!!

Passo 2

Também no Exercício 3.49, nós achamos as distribuições marginais de x e y , sendo descritas abaixo:

g 1 = ∑ y p 1 , y = 0,05 + 0,05 + 0,00 = 0,1

g 2 = ∑ y p 2 , y = 0,05 + 0,1 + 0,2 = 0,35

g 3 = ∑ y p 3 , y = 0,1 + 0,35 + 0,1 = 0,55

Agora, para h ( y ) :

h 1 = ∑ x p x , 1 = 0,05 + 0,05 + 0,1 = 0,2

h 3 = ∑ x p x , 3 = 0,05 + 0,1 + 0,35 = 0,5

h 5 = ∑ x p x , 5 = 0 + 0,2 + 0,1 = 0,3

Sendo assim, podemos encontrar a média de X :

μ X = ∑ x x g ( x )

= ∑ x 3 x g ( x )

= 1 0,1 + 2 0,35 + 3 0,55

μ X = 2,45

De forma similar, a média de Y é:

μ Y = ∑ x y h ( y )

= 1 0,2 + 3 0,5 + 5 ( 0,3 )

μ Y = 3,2

Passo 3

Por fim, podemos definir a covariância pela fórmula do Passo 1.

σ X Y = ∑ x ∑ y x - μ X y - μ Y f ( x , y )

= 1 - 2,45 1 - 3,2 0,05 + 1 - 2,45 3 - 3,2 0,05 + 1 - 2,45 5 - 3,2 0

+ 2 - 2,45 1 - 3,2 0,05 + 2 - 2,45 3 - 3,2 0 , 1 + 2 - 2,45 5 - 3,2 0 , 2

+ 3 - 2,45 1 - 3,2 0 , 1 + 3 - 2,45 3 - 3,2 0 , 35 + 3 - 2,45 5 - 3,2 0 , 1

= 0,1595 + 0,0145 - 0 + 0,0495 + 0,009 - 0,162 - 0,121 - 0,0385 + 0,099

σ X Y = 0,01

Resposta

σ X Y = 0,01

Exercícios de Livros Relacionados

Refira-se ao Exercício 12 e calcule V(Y) e Y. Determine, então, a probabilidade de Y estar dentro do intervalo de 1 desvio padrão em torno da média.
Um fundo de investimento recebe diariamente pedidos de compra de cotas de participação, os quais distribuem-se segundo uma média por pessoa de 2.000 cotas e desvio padrão de 400 cotas. Por outro lado,
Numa chapa são produzidos furos retangulares, cujo comprimento unitário vale em média 200m m , com desvio padrão de 0,6m m . Cada furo deve ser fechado por 4 pinos retangulares iguais e por 1 calço em
O comportamento de componentes em série tem papel fundamental nos problemas de confiabilidade da engenharia e da ciência. A confiabilidade do sistema inteiro certamente não é melhor do que o component
Considere um sistema de componentes no qual há cinco componentes independentes, cada um com uma probabilidade operacional de 0,92. O sistema tem uma redundância que faz com que ele não falhe se três d