Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 53
Suponha que uma mercearia compre cinco caixas de leite desnatado com o preço de atacado de $ 1,20 por caixa e revenda esse leite por $ 1,65 por caixa. Depois da data de validade, o leite não vendido é retirado da prateleira e o dono da mercearia recebe um crédito do distribuidor igual a três quartos do preço de atacado. Se a distribuição de probabilidade da variável aleatória , número de caixas vendidas desse lote, é
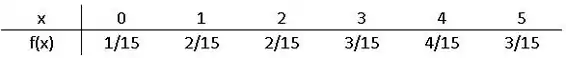
Determine o lucro esperado.
Passo 1
Falaa, meu querido/minha querida. Vamos usar como a variável aleatória que representa o lucro feito pela mercearia.
Se a loja comprar o leite ao preço de $ 1,20 a caixa e vende-lo a $ 1,65 a caixa, isso significa que o lucro é por caixa.
A loja volta do valor que pagaram pela caixa de leite, por cada caixa que não conseguirem vender antes do prazo de validade, portanto, a perda por cada caixa é .
Então, bora para os cálculos!!!
Passo 2
Se é o número de caixas vendidas (entre as 5 caixas compradas), então é o número de caixas que não foram vendidas. Assim, nós temos o lucro total de:
O lucro esperado que queremos encontrar, é a média da variável aleatória , ou seja, . Podemos encontrar esse valor determinando e usando a fórmula abaixo:
Inserindo os valores fornecidos pela tabela podemos encontrar o valor esperado de :
Por fim, podemos encontrar o lucro esperado com a fórmula que definimos acima: