Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 8
Determine a distribuição de probabilidade da variável aleatória W do Exercício 3.3, assumindo que a moeda seja viciada, de modo que cara seja duas vezes mais provável de ocorrer do que uma coroa.
Passo 1
Falaa, meu querido/minha querida. Vamos usar para ser a variável aleatória que dá o número de caras menos o número de coroas em três lançamentos de uma moeda.
Todos os valores possíveis da variável aleatória discreta são:
(3 caras menos 0 coroas)
(2 caras menos 1 coroa)
(1 cara menos 2 coroas)
(0 caras menos 3 coroas)
Então, bora para os cálculos!!!
Passo 2
A moeda é viciada de modo que uma cara tem duas vezes mais probabilidade de ocorrer do que uma coroa. Assim, se o denota o evento em que ocorre uma cara e denota o evento em que ocorre uma coroa, temos:
Então, a probabilidade de cair coroa é:
E a probabilidade cair cara:
Sendo assim, temos as seguintes probabilidades:
Para 3 caras.
Para 2 caras e 1 coroa.
Para 1 cara e 2 coroas.
Por fim, para 3 coroas.
Portanto, a distribuição de probabilidade é definida pela tabela abaixo:
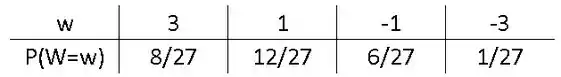
Resposta
Resolução nos passos anteriores.