Uma empresa tem 4 caminhões de aluguel. Sabe-se que o aluguel é feito por dia e que a distribuição diária do número de caminhões alugados é a seguinte:

Calcular:
- O n° médio diário de caminhões alugados, bem como o desvio padrão:
- A média e o desvio padrão do lucro diário, sabendo-se que: valor do aluguel por dia é igual a Cr$ 3.000,00; despesa total diária com manutenção é igual a Cr$ 1.000,00 (quando o caminhão é alugado no dia) e igual a Cr$ 200,00 (quando o caminhão não é alugado no dia).
Passo 1
Olá galerinha! Vem comigo neste exercício!
Uma variável aleatória é sempre associada a seus resultados mutuamente exclusivos a probabilidade. E a variável aleatória é dita discreta quando pode assumir um número finito de valores dentro de um intervalo finito.
A distribuição de probabilidades é uma série de eventos mutuamente exclusivos que constituem a totalidade dos resultados numa experiência aleatória, isto é:
A cada evento , associamos um número real , e teremos como consequência que:
E sabemos que a média de distribuição (), da variável , é a soma dos produtos dos valores da variável pelas respectivas probabilidades, isto é:
E o desvio padrão pela seguinte equação:
Passo 2
Então vamos lá para nosso exercício, então temos o seguinte:
- N° de caminhão alugado por dia;
- probabilidade de alugar o caminhão.
Sabendo disso, conseguimos completar nossa tabelinha:
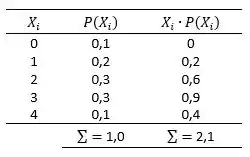
Sendo assim, o número médio diário de caminhões alugados é:
Com o valor da média conseguimos calcular o desvio padrão:

Passo 3
No item b) queremos saber a média e o desvio padrão do lucro diário, sabendo que:
- Aluguel ;
- Despesa se o caminhão é alugado ;
- O lucro quando o caminhão é alugado é
- Despesa se o caminhão não é alugado .
Então teremos o seguinte:
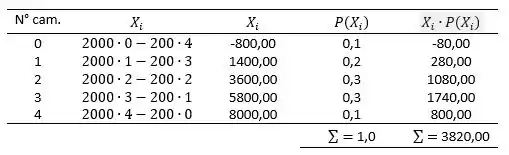
Portanto:
Com a média conseguimos calcular o desvio padrão da seguinte maneira:

Esse foi mais longuinho, mas espero que eu tenha conseguido te ajudar, até mais!
Resposta
- ;
- ;
.
.