Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.1 - Ex. 36
Encontrando probabilidades empíricas: uma empresa está conduzindo uma pesquisa para determinar quão preparadas as pessoas estão para interrupções de energia de longo prazo, desastre natural ou ataque terrorista. A distribuição de frequência na tabela a seguir mostra os resultados. Use-a nos exercícios 35 e 36. (Adaptado de: Harris Interactive.)
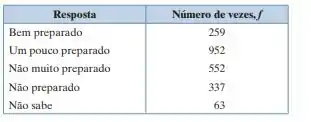
36. Qual é a probabilidade de que a próxima pessoa pesquisada não esteja muito preparada?
Passo 1
O primeiro passo é reconhecer que trata-se de uma probabilidade empírica, pois está sendo feita tomando como base observações coletadas em experimentos anteriores.
Passo 2
O segundo passo, consiste em definir probabilidade empírica:
Probabilidade empírica (ou estatística) é baseada em observações obtidas de experimentos probabilísticos. A probabilidade empírica de um evento E é a frequência relativa do evento E. P(E) = frequência do evento E/ frequência total = f /n
Passo 3
Para finalizar, devemos calcular essa divisão, dando valores a expressão vemos que a frequência relativa das pessoas não muito preparadas é o número 552, e a frequência total consiste na soma das frequências, ou seja, 2.163, então:
552/2163= 0,255
Resposta
0,255