1. Se quisermos realizar um teste tt para duas amostras, exigimos que ambas as distribuições amostrais da média amostral sejam aproximadamente normais.

H

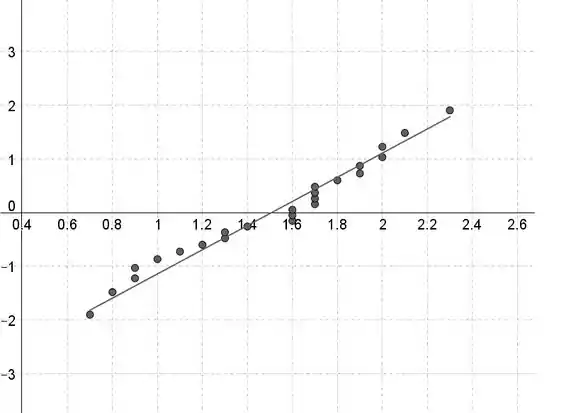
Vamos criar um gráfico de probabilidade normal.

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são as pontuações z na tabela de probabilidade normal do apêndice correspondente a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.



Passo 2

Se o padrão no gráfico de probabilidade normal é aproximadamente linear e não contém curvatura forte, então a distribuição da população é aproximadamente normal.

Ambos os gráficos de probabilidade não contêm curvatura forte e são aproximadamente lineares, portanto, ambas as distribuições populacionais são aproximadamente normais.

Como as distribuições populacionais são aproximadamente normais, a distribuição amostral das médias amostrais também são aproximadamente normais. e, portanto, é apropriado usar o teste t para duas amostras.

2. Classifique todos os valores de dados do menor para o maior:

H: 0,7, 0,8, 0,9, 0,9, 1, 1,1, 1,2, 1,3, 1,3, 1,4, 1,6, 1,6, 1,6, 1,7, 1,7, 1,7, 1,7, 1,8, 1,9, 1,9, 2, 2, 2,1, 2,3

P: 1, 1,1, 1,3, 1,5, 1,5, 1,6, 2,1, 2,6

H

O mínimo é 0.7.

Como o número de valores de dados é par, a mediana é a média dos dois valores centrais do conjunto de dados classificado:

O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):

O terceiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados)

O máximo é 2.3.

O mínimo é 1.

Como o número de valores de dados é par, a mediana é a média dos dois valores centrais do conjunto de dados classificado:

O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):

O terceiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados):

O máximo é 2.6.

Passo 3

Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no primeiro quartil, termina no terceiro quartil e tem uma linha vertical na mediana.

O primeiro quartil está em 25% da lista de dados classificados, a mediana em 50% e o terceiro quartil em 75%.



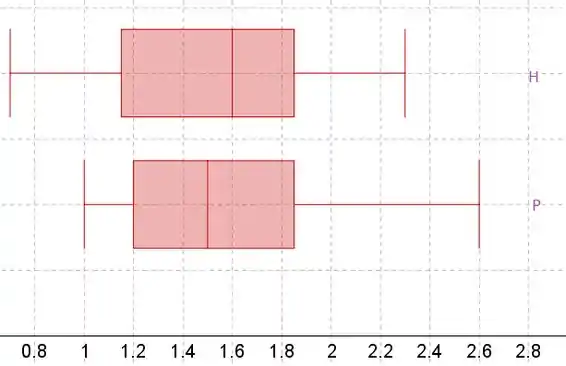
Parece haver uma pequena diferença entre a verdadeira extensibilidade média para amostras de tecido de alta qualidade e para amostras de baixa qualidade, porque a linha vertical na caixa do boxplot não está aproximadamente na mesma posição em ambos os boxplots.

Vamos supor: α=0.05

Reivindicação dada: difere

A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter o valor mencionado na reivindicação.

Determine a estatística de teste:

Determine os graus de liberdade (arredondados para o inteiro mais próximo):

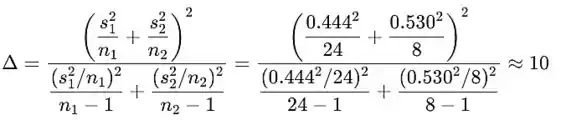
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha df=10:

Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:

Não há evidências suficientes para apoiar a alegação de que a extensibilidade média real difere para os dois tipos de tecido.