Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 32

No Exercício 3.13, a distribuição do número de imperfeições por dez metros de um tecido sintético é dada por

(a) Faça um gráfico da função de probabilidade.

(b) Determine o número esperado de imperfeições, E ( X )   =   μ

(c) Determine E ( X 2 ) .

Passo 1

Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!

Vamos fazer o gráfico da função de probabilidade:

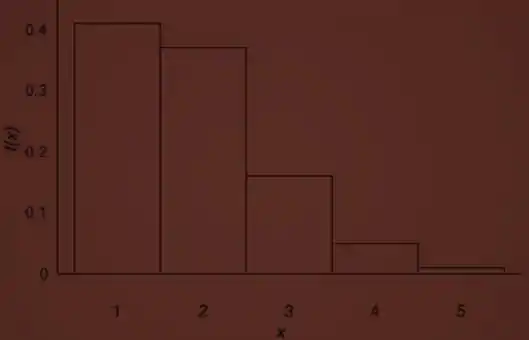
Passo 2

Agora vamos resolver o item b), queremos o valor esperado E ( X )

Primeiro, lembremos que:

E X = ∑ x p ( x )

Logo,

E X = 0 0,41 + 1 0,37 + 2 0,16 + 3 0,05 + 4 0,01 = 0,88

Passo 3

Agora vamos ao item c)

Neste item queremos E X 2

Lembrando da relação no valor esperado, temos que:

E g ( x ) = ∑ g ( x ) p ( x )

Logo:

E X 2 =   0 2 0,41 + 1 2 0,37 + 2 2 0,16 + 3 2 0,05 + 4 2 0,01 = 1,62

Resposta

  1. Vide gráfico
  2. E X = 0,88
  3. E X 2 = 1,62

Exercícios de Livros Relacionados

Uma loja de eletrodomésticos vende três modelos diferentes de freezers verticais com 13,5, 15,9 e 19,1 pés cúbicos de espaço, respectivamente. Seja X = volume de armazenagem comprado pelo próximo clie
O resultado denominado desigualdade de Chebyshev diz que, para qualquer distribuição de probabilidade de uma va X e qualquer número k ao menos igual a 1, P(|X- μ |)k σ ) a. Qual é o valor do limite su
Uma pequena drogaria solicita cópias de uma revista para seu display todas as semanas. Represente por X = demanda da revista, com fmpSuponha que o proprietário da loja pague US$ 1,00 por cópia e o pre
a. Desenhe um gráfico de linhas da fmp de X do Exercício 34. Determine, então, a fmp de X e desenhe seu gráfico de linhas. Considerando as duas situações, o que você pode dizer sobre V(X) e V(X)? b. U
Refira-se ao Exercício 12 e calcule V(Y) e Y. Determine, então, a probabilidade de Y estar dentro do intervalo de 1 desvio padrão em torno da média.