Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 2.Exercícios propostos - Ex. 11
Uma pessoa está querendo ouvir uma melodia que sabe estar gravada numa das 8 faixas de um disco. Como não se sabe em qual das faixas está a melodia gravada, ele experimenta a 1ª faixa, depois a 2ª, e assim sucessivamente, até encontrar a melodia procurada. Qual o número médio e o desvio padrão do número de faixas que deverá tocar até encontrar a melodia procurada?
Passo 1
Olá galerinha, tudo bem com vocês? Vamos lá para mais um exercício?!
Uma variável aleatória é sempre associada a seus resultados mutuamente exclusivos a probabilidade. E a variável aleatória é dita discreta quando pode assumir um número finito de valores dentro de um intervalo finito.
A distribuição de probabilidades é uma série de eventos mutuamente exclusivos que constituem a totalidade dos resultados numa experiência aleatória, isto é:
A cada evento , associamos um número real , e teremos como consequência que:
E sabemos que a média de distribuição (), da variável , é a soma dos produtos dos valores da variável pelas respectivas probabilidades, isto é:
E o desvio padrão pela seguinte equação:
Passo 2
Pelo enunciado, sabemos que a probabilidade de acertarmos a música em cada faixa é:
Então temos os seguintes dados:
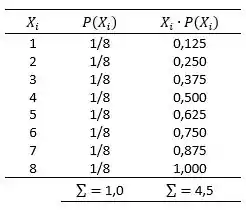
Sendo assim nossa média é:
Para descobrirmos o desvio padrão, vamos calcular o valor de para cada :
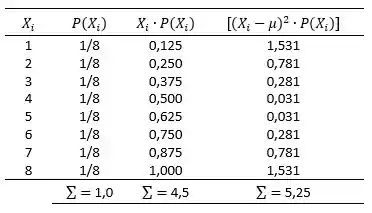
O desvio padrão será:
Resposta
;
.