Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.1 - Ex. 3d
A quantia gasta anualmente, em milhões de reais, na manutenção do asfalto em uma cidade do interior é representada pela variável com densidade dada por:
d. A mediana de
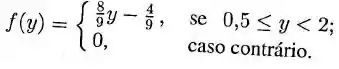
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para calcular o valor esperado e a variância de com base na função densidade de probabilidade dada, lembrando que fora do intervalo elas são nulas. Certo?
Pois bem, você se lembra desse conceito? Porque se não, é hora de dar aquela revisão!
Bora então resolver esse exercício?
Passo 2
A mediana, como vimos nesse capítulo, é o valor tal que e
Desta forma,
Mas,
Resposta
Assim, concluímos o que nos foi pedido.
Exercícios de Livros Relacionados
Seja X o tempo que um livro de uma reserva de duas horas, na biblioteca de uma faculdade, é examinado por um estudante selecionado aleatoriamente e suponha que X tenha função de densidade f x = f x =
Suponha que o erro envolvido ao se fazer uma certa medida seja uma va contínua X com fdp f x = 0,09375 ( 4 - x 2 ) , - 2 ≤ x ≤ 2 0 ,c a s oc o n t r á r i o á a. Faça o gráfico de f(x).b. Calcule P (
Suponha que a temperatura de reação X (em °C), em um certo processo químico, tenha função de densidade uniforme para A = -5 e B = 5 .a. Calcule P ( X0 ) .b. Calcule P - 2,5X2,5 .c. Calcule P ( - 2 ≤ X
Seja X a tensão de vibração1 (psi). Em uma palheta de turbina com certa velocidade de vento em um túnel aerodinâmico. O artigo “Blade Fatigue Life Assessment with Application to VAWTS” (J. Solar Energ
94. Seja X o tempo até a falha (em anos) de certo componente hidráulico. Suponha que a fdp de X seja f(x) = 32/(x 4)³ para x0. a. Demonstre que se f(x) é uma fdp legítima. b. Determine a fdc. c. Use o