Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 8

O salário médio dos empregados das indústrias siderúrgicas de um país é de 2,5 salários

mínimos, com um desvio padrão de 0,5 salários mínimos. Uma indústria é escolhida ao

acaso e desta é escolhida uma amostra de 49 empregados, resultando um salário médio de

2,3 salários mínimos. Podemos afirmar que esta indústria paga salários inferiores à média

nacional, com o nível de 5%?

Passo 1

Temos: X = s a l á r i o   d o s   e m p r e g a d o s   d a s   i n d u s t r i a s   s i d e r u r g i c a s   S M

Considerando que a população de trabalhadores nesta indústria seja normalmente distribuída:

X ~ N ( 2,5   ; 0,5 2 )

Podemos usar a seguinte aproximação:

Z = X - - μ σ 2 n ~ N ( 0,1 )

Do enunciado, temos o seguinte:

X - = 2,3   s m   e   n = 49   e m p r e g a d o s .

Adotando α = 5 %

Passo 2

Teste de Hipótese: H 0 : μ = 2,5     e     H 1 :   μ < 2,5

Vamos construir nossa região crítica:

R C = z 0 ∈ R z 0 < - z α }

Com z 0,05 = 1,64

Logo,

R C = { z 0 - 1,64 }

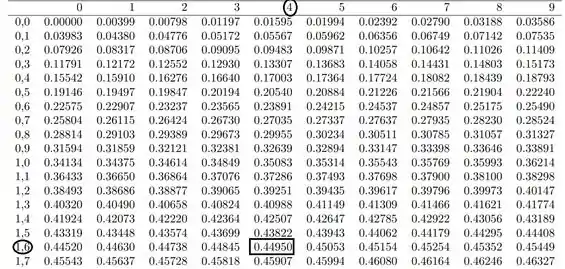
Lembrando que na tabela de distribuição normal, quando temos uma RC unilateral:

p = 0,5 - α = 0,45 .

Passo 3

Teste sob H 0 :

z 0 = 2,3 - 2,5 0,5 2 49 = - 2,80

Resposta

Como, z 0 = - 2,80 ∈ R C , rejeitamos H 0 e concluímos que existem evidencias de que a indústria selecionada paga salários inferiores à média nacional aos seus empregados.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supõe-se que determinado tipo de indústria deva ter, em média, 30 empregados. Para testartal hipótese, colhe-se uma amostra de 50 indústrias, cujo resultado está abaixo. Caso rejeitea hipótese, dê um
Uma fábrica de automóveis anuncia que seus carros consomem, em média, 11 litros por100 km, com desvio padrão de 0,8 litro. Uma revista resolve testar essa afirmação eanalisa 35 automóveis dessa marca,
De uma população X~ N ( 50 ,100 ) retira-se uma amostra de dez elementos e calculam-se osvalores de σ * 2eS 2 . Encontre os valores pedidos abaixo, com a maior precisão possível.(a) P σ * 2a = 10 % en
O número médio diário de clientes de um posto de gasolina tem sido 250, com um desviopadrão de 80 clientes. Durante uma campanha de 25 dias, em que os clientes recebiamum brinde, o número médio de cli
O custo X de manutenção de teares segue uma distribuição normal, X ~ N ( μ ,400 ) . Durante muito tempo, o parâmetro μ tem sido adotado como igual a 200. Suspeita-se que esse parâmetro aumentou, e só