Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 27b

Primeiro, vamos sempre lembrar do seguinte, se , podemos usar a seguinte aproximação para a variável:

Que é a normal padrão.

Então, seja uma probabilidade:

É a aproximação pela normal padrão.

Vamos ter, para , o seguinte:

Dando uma ajeitada:

Em outras palavras, estamos buscando:

Como é um valor alto, algumas tabelas talvez nem tenham, sabendo que , podemos aproximar:

Já o outro valor, convém buscarmos na tabela:

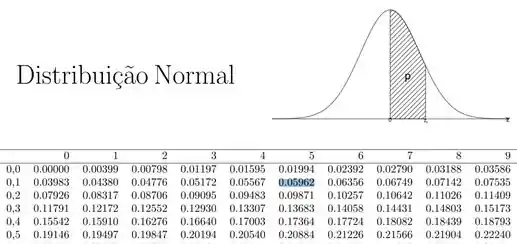
Portanto:

Concluimos:

(b)