Enunciado
Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 4.Problemas - Ex. 13
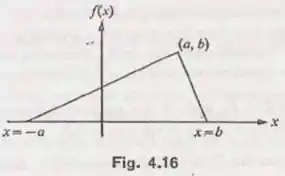
Suponha que o gráfico na Fig. 4.16 representa a fdp de uma variável aleatória .
a) Qual será a relação entre e .
b) Se e , que se pode dizer do maior valor que pode tomar?
Passo 1
Observe que o gráfico da fdp forma um triângulo com o eixo . A base do triângulo é
Já a altura é
Assim, a área é
Para que a função seja uma fdp, a área deve ser 1:
Essa é a relação entre e !
Passo 2
Isolando , achamos
Como , segue que
Multiplicando a inequação por :
Logo,
Mas como é suposto positivo no enunciado do item (b), o maior valor que pode tomar é
Resposta
Exercícios de Livros Relacionados
Uma indústria usa um esquema de aceitação emseus itens de produção antes de serem transportados. Oplano é feito em duas etapas. Caixas com 25 itens sãopreparadas para o transporte e uma amostra de trê
Uma empresa está interessada em avaliar seu procedimento atual de inspeção de carregamentos de 50itens idênticos. O procedimento é retirar uma amostrade cinco itens e liberar o carregamento se não mai
Se uma pessoa recebe 13 cartas de um baralho comum com 52 cartas, quantas cartas de copas são esperadas? Entre quais dois valores você esperaria que o número de copas estivesse pelo menos em 75% do t
Estudos sobre populações na biologia e no meio ambiente freqüentemente capturam, colocam uma etiquetacom identificação e soltam os animais para estimar o tamanho e o grau de certas características em
Uma força-tarefa do governo suspeita que algumasindústrias violam as regulamentações federais contra poluição, em relação ao despejo de certo tipo de produto.Vinte empresas estão sob suspeita, mas não