Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 58

Suponha que X e Y sejam variáveis aleatórias independentes que têm como distribuição de probabilidade conjunta

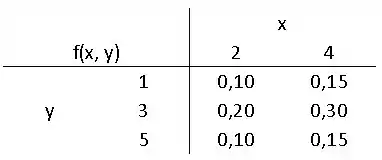
Determine

(a) E ( 2 X - 3 Y ) ;

(b) E ( X Y ) .

Passo 1

Falaa, meu querido/minha querida. Lembrando que para calcularmos o valor esperado de uma variável discreta usamos a fórmula abaixo:

E X = ∑ x ∑ y x f ( x , y )

Então, bora para os cálculos!!!

Passo 2

Calculando o valor esperado de X :

E X = ∑ x x ∑ y f ( x , y )

= 2 f 2 ,   1 + f 2 ,   3 + f 2 ,   5 + 4 f 4 ,   1 + f 4 ,   3 + f 4 ,   5

= 2 0,10 + 0,20 + 0,10 + 4 ( 0,15 + 0,30 + 0,15 )

E X = 3,2

Calculando o valor esperado de Y :

E Y = ∑ x y ∑ y f ( x , y )

= 1 f 2 ,   1 + f 4 ,   1 + 3 f 2 ,   3 + f 4 ,   3 + 5 f 2 ,   5 + f 4 ,   5

= 1 0,10 + 0,15 + 3 0,20 + 0,30 + 5 0,10 + 0,15

E Y = 3

Sendo assim, o valor esperado que o enunciado nos pede E ( 2 X - 3 Y ) é:

E 2 X - 3 Y = E 2 X - E 3 Y = 2 E X - 3 E ( Y )

= 2 3,2 - 3 ( 3 )

E 2 X - 3 Y = - 2,6

Passo 3

Por fim, como as variáveis X e Y são independentes, nós podemos usar a seguinte relação:

E X Y = E X E Y = 3,2 3 = 9,6

Resposta

(a) E 2 X - 3 Y = - 2,6

(b) E X Y = 9,6

Exercícios de Livros Relacionados

Suponha que X eY tenham a seguinte distribuição conjunta:c) Mostre que, embora E ( X Y )=E ( X )E ( Y ), X e Y não são independentes.
Dada à distribuição conjunta de X e Y abaixo, determine a média e a variância de:b) X Y .
Suponha que X eY tenham a seguinte distribuição conjunta:b) Determine a f.p. de X Y e, em seguida, calcule E ( X Y ) .
Seja X uma variável aleatória binomial com p=0.25 e n=3. Encontre a distribuição de probabilidades da variável aleatória Y=X^2
Suponha que X seja uma variável aleatória com distribuição de probabilidade f X ( X ) = 1 4 para 1,2,3,4Encontre a distribuição de probabilidade de Y=2X+1