Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 13b
A tabela de frequência apresentada em seguida está incompleta e contêm observações das variáveis: vida útil do equipamento (U) e garantia do fabricante (G), ambas medidas em anos.
- Complete a tabela.
- Construa o gráfico U por G e verifique se há associação entre as variáveis.
- Calcule a vida útil média para cada subgrupo de valor da garantia. Comente os resultados.
Passo 1
- Para construir o gráfico, vamos montar um gráfico conforme o modelo do livro desse capitulo marcando os pontos nos pares e colocando o valor de suas frequências ao lado dos pontos, então nossa tabela tinha ficado com a seguinte cara da letra (a):
Passo 2
Montando o gráfico:
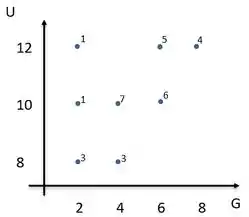
Passo 3
Existe associação entre as variáveis, porque o gráfico nos mostra que o comportamento da vida útil dos equipamentos cresce conforme a garantia também aumenta.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Empregue a fgm para mostrar que, se X e Y forem variáveis aleatórias independentes, com distribuição N ( μ x , σ x 2 ) e N μ y ,σ y 2 , respectivamente, então Z = a X + b Y será também normalmente dis
Alguns resistores, Ri, i = 1,2,...,n, são montados em série em um circuito. Suponha que a resistência de cada um seja normalmente distribuída, com E R i = 10 e V R i = 0,16 .Se n=5, qual será a probab
10-5. Dois tipos de plásticos são adequados para uso por um fabricante de componentles eletrónicos. A resisténcia à quebra desse plástico é importante. É de tamanho a. A companhia não adotará o plásti
10-8. Um polímero é fabricado em uma batelada de um processo quimico. Medidas de viscosidade são normalmente feitas em cada batelada e a longa experiéncia com o processo tem indicado que a variabilida
10-10. Considere o teste de hipóteses Suponha que os tamanhos de amostra sejam n, = 15 e que os dados sejam retirados de distribuições normais.Use a(a) Teste a hipxitese e encontre o valor P.(b) Expli