Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 30a
Um teste de aptidão feito por pilotos de aeronaves em treinamento inicial requer que uma série de operações seja realizada em uma rápida sucessão.
Suponha que o tempo necessário para completar o teste seja distribuído de acordo com uma normal de média e desvio padrão de
- Para passar no teste, o candidato deve completa-lo em menos de 80 minutos. Se 65 candidatos tomam o teste, quantos são esperados passar?
Passo 1
Antes de tudo, vamos definir nossas variáveis:
E
Perceba que,
Enquanto:
Na alternativa A precisamos obter da binomial, será dado por:
Agora, se você se lembrar, usamos a seguinte aproximação pela normal padrão para :
Então, na probabilidade:
Passo 2
Portanto:
Lembrando que, na verdade buscamos:
Onde, devido ao fato do gráfico ser simétrico e portanto cada lado terá :
Agora, buscando na tabela de distribuição normal:
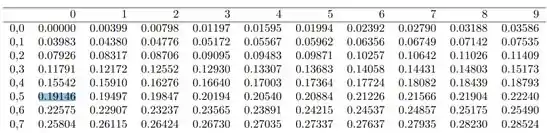
Encontramos:
Portanto:
E agora, perceba que é a probabilidade de alguém concluir o teste em menos de
Precismos agora, obter quantos dentre pilotos, consiguirão tal feito:
Passo 3
Buscamos então o valor de esperado de sabendo que
Se você se lembrar, o valor esperado de um variável com modelo binomial é dado por:
Portanto:
Resposta
Concluimos que dentre 65 candidatos, esperamos que 20 deles obtenham um tempo menor do que no teste.