Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 53

Três cartas são retiradas, sem reposição, de 12 cartas com figuras (valetes, damas e reis) de um baralho comum de 52 cartas. Considere X o número de reis selecionados e Y , o número de valetes. Determine

(a) a distribuição de probabilidade conjunta de X e Y;

(b) P [ ( X ,   Y ) ∈ A ] , onde A é a região dada por { ( x ,   y ) | x + y ≥ 2 } .

Passo 1

Falaa, meu querido/minha querida. Como há 4 reis e 4 valetes no total, e 3 cartas estão sendo sorteadas, sabemos que as variáveis ​​aleatórias X e Y podem assumir os valores 0,1,2 e 3.

Já podemos concluir que:

P X = 3 , Y = 1 = P X = 3 ,   Y = 2 = P X = 3 ,   Y = 3 = 0

P X = 2 ,   Y = 2 = P X = 2 ,   Y = 3 = P X = 1 ,   Y = 3 = 0

Essas probabilidades acima sugerem que mais de 3 cartas são retiradas, o que é falso.

Então, bora realizar a questão!!!

Passo 2

Notamos que, se o sorteio contém x reis e y valetes, também contém 3 - x - y rainhas. Portanto, o número de maneiras pelas quais x reis e y valetes podem ser escolhidos na amostra é:

4 x 4 y 4 3 - x - y

Para todo par ( x , y ) sendo x + y ≤ 3 .

Sabendo que o número total de maneiras pelas quais podem ser retiradas 3 cartas de 12 é 12 3 , encontramos a fórmula abaixo:

f x ,   y = P X = x ,   Y = y = 4 x 4 y 4 3 - x - y 12 3

Inserindo todas as combinações que não resultam em 0 na equação acima, encontramos a tabela a seguir:

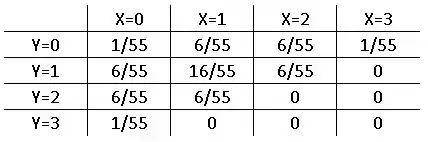
Passo 3

Levando em conta a tabela de distribuição de probabilidade conjunta, temos:

P X ,   Y ∈ A = P ( X + Y ≥ 2 )

= 1 - P ( X + Y < 2 )

= 1 - P ( X + Y ≤ 1 )

= 1 - P X = 0 , Y = 0 + P X = 1 ,   Y = 0 + P X = 0 ,   Y = 1

= 1 - 1 55 + 6 55 + 6 55

P X ,   Y ∈ A = 42 55

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Se a distribuição de probabilidade conjunta de X e Y é dada por f x , y = x + y 30 ,x = 0 ,1 ,2 ,3 ; y = 0 ,1 ,2 , Determine(a) P ( X ≤ 2 ,Y = 1 ) ;(b) P ( X2 ,Y ≤ 1 ) ;(c) P ( XY ) ;(d) P X + Y = 4 .
Considere um experimento que consiste em duas jogadas de um dado balanceado. Se X é o número de resultados quatro e Y é o número de resultados cinco obtidos em duas jogadas do dado, determine(a) a dis
Suponha que X e Y tenham a seguinte distribuição de probabilidade conjunta:(a) Determine a distribuição marginal de X.(b) Determine a distribuição marginal de Y.
Determine os valores de c de modo que as seguintes funções representem as distribuições de probabilidade conjuntas das variáveis aleatórias X e Y:(a) f x ,y = c x y , para x = 1 ,2 ,3 ; y = 1 ,2 ,3 ;(
Referindo-se ao Exercício 3.38, determine(a) a distribuição marginal de X;(b) a distribuição marginal de Y.