Três moléculas do tipo A, três do tipo B, três do tipo C e três do tipo D serão vinculadas uma à outra para formar uma cadeia molecular. Uma molécula desse tipo é ABCDABCDABCD e outra é BCDDAAABDBCC.

a) Quantas moléculas desse tipo podem ser formadas? (Sugestão: se as três moléculas A forem diferentes uma da outra –A1, A2 e A3 – assim como as B, C e D, quantas moléculas haverá? Como esse número será reduzido se não houver distinção entre as moléculas A?)

b) Suponha que uma molécula composta do tipo descrito seja selecionada aleatoriamente. Qual é a probabilidade de que todas as moléculas de cada tipo estejam juntas (como em BBBAAADDDCCC)?

Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!

Vamos estudar os dois casos supracitados.

Se os A's são distinguíveis uns dos outros, e da mesma forma para os B's, C's e D's,

então são moléculas de cadeia possíveis. De acordo com a regra do produto.

Seis deles são:

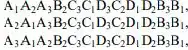
Esses 6 (=3!) diferem apenas no que diz respeito à ordenação dos 3 A’s. Em geral, grupos de 6

moléculas de cadeia podem ser criadas de tal forma que dentro de cada grupo apenas a ordenação dos A's é diferente. Quando os subscritos A são suprimidos, cada grupo de 6 “colapsa” em uma molécula única (B’s, C’s e D’s ainda são distinguíveis). Neste ponto há moléculas. Agora, suprimir os subscritos nos B’s, C’s e D’s, por sua vez, dá em última análise moléculas de cadeia.