Umaa concessionária tem disponível, para um certo automóvel, os modelos com duas versões de combustível, álcool ou gasolina. Com motor a álcool os preços são e mil reais para os modelos e respcctivamente. Esses preços são superiores se o combustível for gasolina. A procura por carros a álcool é, de e a gasolina Qualquer
Que seja o combustível escolhido há igual preferência entre os modelos. Calcule a função de probabilidade do preço desse automóvel e obtenha sua média e variância.
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
Mas antes, vamos construir a árvore de probabilidades para esse problema. Ok?
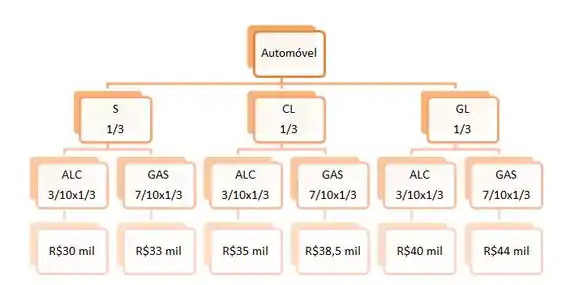
Passo 2
Agora, seja a variável aleatória preço do automóvel.
A função de probabilidade tem a seguinte distribuição:

Passo 3
E calculando a esperança (média do preço desse automóvel), temos que:
Calculando agora temos:
Assim,
Resposta
Logo, concluímos o que nos foi pedido no enunciado.