Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 54

X e Y são variáveis aleatórias normais e independentes, com

Determine o seguinte:

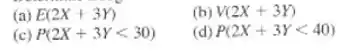
Passo 1

X e Y são independentes, variáveis aleatórias normais com E ( X ) = 0 ,   V ( X ) = 4 ,   E ( Y ) = 10 ,   e V ( Y ) = 9

Letra a:

Vamos calcular E ( 2 X + 3 Y ) :

E ( 2 X + 3 Y ) = E ( 2 X ) + E ( 3 Y ) = 30

Passo 2

Letra b:

Vamos determinar V ( 2 X + 3 Y ) :

V ( 2 X + 3 Y ) = 2 2 V ( X ) + 3 2 V ( Y ) = 97

Passo 3

Letra c:

Vamos calcular P ( 2 X + 3 Y < 30 )

Uma combinação linear de duas variáveis ​​aleatórias normais independentes também é uma

variável aleatória normal, ou seja 2 X + 3 Y ∼ N ( 30,97 )

Da simetria da curva normal:

P ( 2 X + 3 Y < 30 ) = P ( z < 30 - 30 97 ) = P ( z < 0 ) = 0.5

Passo 4

Letra d:

Vamos encontrar P ( 2 X + 3 Y < 40 ) . Seja:

z = 2 x + 3 Y - 30 97

P ( 2 X + 3 Y < 40 ) = P ( Z < 1.02 ) = 0.8461

Resposta

  1. 30
  2. 97
  3. 0.5
  4. 0.8461
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que X seja uma variável aleatória contínua com distribuição de probabilidades f X ( x ) = x 18 ,0 ≤ x ≤ 6 Encontre a distribuição de probabilidades da variável aleatória Y=2X+10Encontre o valo
Suponha que X tenha uma distribuição de probabilidades uniformes f X ( x ) = 1 ,0 ≤ x ≤ 1 Mostre que a distribuição de probabilidades da variável aleatória Y= -2lnX é uma variável qui-quadrado com doi
Na fabricação de lâmpadas de eletroluminescência, para as camadas diferentes de tinta são depositadas em um substrato plástico. A espessura dessas camadas é crítica se especificações relativas a cor f
Se X e Y têm uma distribuição normal bivariada com rho =0, mostre que X e Y são independentes
Suponha que X e Y tenham uma distribuição normal bivariada, com função densidade de probabilidade conjunta.mostre que a distribuição condicional de Y, dado que X=x, é normal.Determine E ( Y | X = x )