Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

O Poder do Teste

Ver Todos os Exercícios

Teoria

Até agora nós falamos bastante do α (erro tipo I) e pouco do β né? Acontece que o α nós geralmente fixamos para conseguir encontrar tanto o ponto crítico quanto a região crítica, enquanto o β (erro tipo II) nós geralmente não conseguimos calcular.

Vamos ver isso melhor através de um exemplo pode ser?

Ex.:

Imagine que temos uma balança de alimentos utilizada para preencher potes de suplementos, em que a v.a. X descreve o peso de cada alimento. Essa v.a. X tem distribuição normal com média μ e variância 400 . A máquina foi regulada para μ = 500 g . Desejamos, periodicamente, colher uma amostra de 16 potes e verificar se a produção está sob controle, ou seja, se μ = 500 g ou não.

H 0 : μ = 500 g

H 1 : μ ≠ 500 g

E terá uma distribuição

X   ~   N μ , σ 2 n

X   ~   N   500 , 400 16

X   ~   N ( 500,25 )

Fixando α = 0,01 teremos que a amostra será rejeitada quando μ for muito grande ou muito pequeno. Percebe que aqui nós temos o caso bilateral, portanto estamos querendo descobrir quais são as duas regiões críticas.

  • μ < 500

    • P x - < x c - 1   x -   ~   N 500,25 = α 2 = 0,005

    P x - - 500 25   < x c 1 - - 500 25 = 0,005

    P Z < x c 1 - - 500 25 = 0,005

    Agora precisamos olhar a tabela normal

    P Z < - 2,58 = 0,0 05

    Então

    x c 1 - - 500 5 = - 2,58

    x c 1 - = 487,1

  • μ > 500

P x - > x c - 2   x -   ~   N 500,25 = α 2 = 0,0 05

P x - - 500 25   > x c 2 - - 500 25 = 0,0 05

P Z > x c 2 - - 500 25 = 0,0 05

Vendo na tabela temos:

P Z > 2,58 = 0,0 5

x c 2 - - 500 5 = 2,58

x c 2 - = 512,9

Assim temos R C = { x - ∈ R   | x - ≤ 487,1   o u   x - ≥ 512,9 }

No gráfico:

R A = { x - ∈ R   | 487,1 ≤ x - ≤ 512,9 }

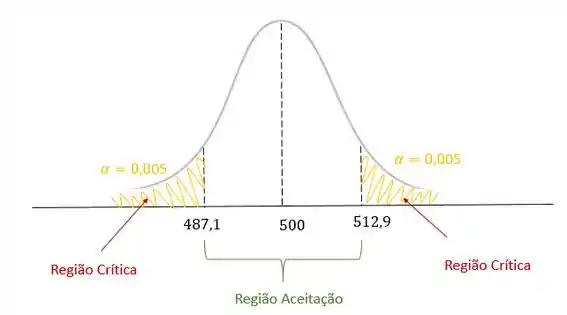
A probabilidade de β não pode ser calculada a menos que se especifique o valor alternativo para μ . Ou seja, quando montamos:

H 0 : μ = 500 g

H 1 : μ ≠ 500 g → T e m o s   q u e   d e f i n i r   u m   μ .

Sabemos que

P e r r o   I I = P a c e i t a r   H o H 1 = P a c e i t a r   H o μ = β

Podemos dizer que β é uma função de μ e escrever

β μ = P ( E s t a r   n a   R e g i ã o   d e   A c e i t a ç ã o | μ )

No exemplo acima, se μ = 505 ficaríamos com:

β μ = P x - ∈ R A   μ )

β μ = P 487,1 ≤ x - ≤ 512,9     μ )

Usando o fato que x -   ~   N 505,25 agora, teremos

β μ = 487,1 - 505 5 ≤ x - - 505 5 ≤ 512,9 - 505 5

β μ = - 3,58 ≤ Z ≤ 1,58 = 94,28 %

Para qualquer outro valor de μ podemos encontrar o respectivo valor de β .

Vamos olhar o quadro de decisões:

Decisão

Valor Real do parâmetro

H o : μ = 500

H 1 : μ ≠ 500

A máquina está sob controle: μ = 500

Probabilidade de estar na região de aceitação, ou seja aceitar H 0   dado que o H o é verdadeira. P R A H o = 0,99

Probabilidade de estar na região de aceitação, de aceitar H o sendo que H 1 é verdadeira. P R A   H 1 = β

(dependendo de valor alternativo de μ )

A máquina não está sob controle: μ ≠ 500

Probabilidade de estar na região Crítica e aceitar H o

P e r r o I = P R C H 0 = 0,01

Probabilidade de rejeitar H 0 sendo que H 1 é verdadeira.

P R C H 1 = 1 - β

(dependendo de valor alternativo de μ )

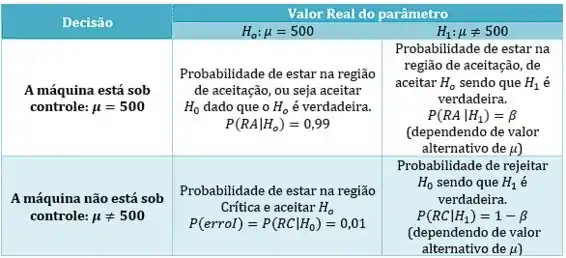
Chamamos P R C H 1 = 1 - β de poder do teste ou potência do teste e representamos por:

π μ = P R C H 1 = 1 - β ( μ )

Exemplo do pote de suplemento teríamos

π 505 = 1 - β 505 = 1 - 0,9428 = 0,0572  

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006 - pp. 341-15.

Sendo X o custo de manutenção de tear, sabe-se que X   ~   N ( μ , 400 ) . Para testar a hipótese:

H 0 : μ = 200

H 1 : μ > 200

Será usada uma amostra de 25 teares. (Considere que o custo não pode ser menor que 200.)

a) Fixando α = 5 %   , encontre a correspondente RC.

c) Para que valores de μ = 210 , qual o poder do teste ?

Passo 1

Fixando α = 0,05 e considerenado H o verdadeira teremos

x -   ~   N ( μ , σ 2 n )

x -   ~   N ( 200 , 400 2 5 )

Passo 2

P e r r o I = P x - ∈ R C H 0   é   v e r d a d e i r a = α

α = P x - > 200 x -   ~   N 200 , 400 25

Passo 3

α = P x - - 200 4 > x c - - 200 4

Queremos

P Z > Z α = P Z > z 0,05

Sabemos que

Z 0,05 = 1,645

Passo 4

Encontrando x c -

x c - - 200 4 = 1,645

x c - = 206,58

A região crítica será:

R C = { x ∈ R   | X > 206,58 }

Passo 5

O poder do teste é β ( μ ) . Para calcular ele, precisamos de valores para μ e também de qual é a região de aceitação

R A = { x ∈ R   | 200 ≤ X ≤ 206,58 }

β μ = P x - ∈ R A   μ )

- - μ = 210  

β μ = 200 - 210 4 ≤ x - - 210 4 ≤ 206,58 - 210 4

β μ = ( - 2,5 ≤ Z ≤ - 0,855 )

β μ = 0 , 1775

π μ = 1 - β μ = 0,8225

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

João Ismael D. Pinheiro, Probabilidade e Estatística

Num certo banco de dados, o tempo para a realização das buscas é aproximadamente normal com média 53   s e desvio padrão 14   s . Modificou-se o sistema para reduzir o tempo. Foram contados os tempos para   30 buscas. Admita que as 30   observações possam ser consideradas uma amostra aleatória e que não houve alteração na variância. Use = 1 % .   Calcule o poder do teste se a verdadeira média de tempo fosse de 45 s .

Passo 1

Sabemos que o poder do teste é π μ = 1 - β ( μ ) ,

Onde:

β μ = P e r r o   t i p o   I I = P ( x - ∈ R A | H 1   v e r d a d e i r a )

Vamos estipular nossas hipóteses então, aqui o objetivo foi reduzir o tempo médio das buscas, que originalmente era de 53 s , então:

H 0 :   μ = 53

H 1 :   μ < 53

Assim estamos testando de fato se a média diminuiu.

Sabemos também que:

x - ~ N 53 ; 14 30

Passo 2

Para achar a RC, e consequentemente a RA, precisamos do nosso x - c r i t i c o , e, para isso, precisamos do z c r í t i c o . Aqui no teste unilateral inferior para média ele é:

z c r í t i c o = - z 1 - α

Como α = 0,01 :

z c r í t i c o = - z 1 - 0,01 = - z 0,99 = - 2,33

Então para achar o x - c r i t i c o , fazemos as operações inversas da padronização no z c r í t i c o (estamos “despadronizando”):

x - c r i t i c o = z c r í t i c o × σ n + μ

Sabemos pelo enunciado que μ = 53 ,   σ = 14 ,   n = 30 , substituindo:

x - c r i t i c o = - 2,33 × 14 30 + 53 = 47,05

Então nossas regiões são:

R C = {   x - < 47,05 }

R A = {   x - > 47,05 }

Passo 3

Então a probabilidade de erro tipo II vai ser, para a verdadeira média de 45 s :

β μ = 45 = P ( x - > 47,05 | μ = 45 )

= P Z > 47,05 - 45 14 30 = P Z > 0,8 = 1 - P Z < 0,8 = 1 - 0,7881 = 0,2119

Então o poder do teste será:

π μ = 1 - 0,2119 = 0,7881

Resposta

0,7881

Exercícios de Livros Relacionados

Um artigo no periódico Journal of Manufacturing Systems (Vol. 10, 1991, pp. 32-40) descreve um experiment para investigar o efeito de quatro fatores P = pressão do jato de água. F = velocidade transve
O tratamento térmico de peças metálicas é um processo largamente utilizado. Um artigo no Journal of Metals (Vol. 41, 1989) descreve um experimento para investigar a distorção do achatamento provenient
Construa um planejamento 2 I V 4 - 1 para o problema do Exercicio 14.57 . Selecione os dados para as oito corridas requeridas para esse planejamento. Analise essas corridas e compare suas conclusões c
Um artigo no periódico IEEE Transactions on Componentes, Hybrids and Manufacturing Technology (1992, Vol.15) descreve um experiment para investigar um método de alinhamento de chips ópticos em placas
Em seu livro Empirical Model Building and Response Surfaces – Construção de Modelos Empíricos e Superfícies de Resposta. (John Wiley, 1987). G. E. Box e N. R. Draper descrevem um experimento com três