Teoria
Fala aí! Bora aprender como calcular o p-valor de uma vez por todas?!
O que Significa p-valor ou Valor de p
Mas antes de qualquer coisa a gente precisa entender o que é p-valor, também chamado de valor de p! O p-valor (ou valor p) é uma forma de resolver os testes hipótese e que permite comparar com o nível de significância, e assim determinar se vamos ou não rejeitar uma hipótese nula.
Após calculado o p-valor é comparado ao nível de significância (
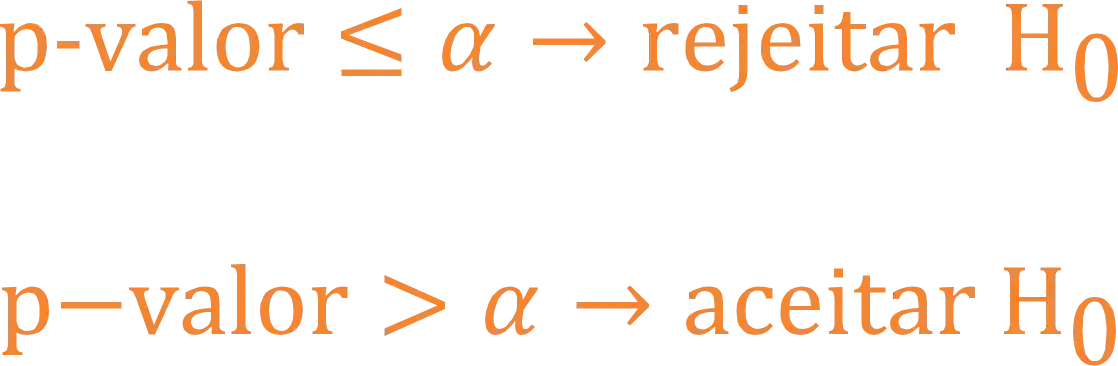
Matematicamente falando, o p-valor é a área abaixo da curva normal na região em que a hipótese nula é rejeitada, o detalhe é que os pontos críticos são dados pelos testes de hipótese. Porém, a forma exata de calcular o p-valor vai depender do tipo de teste de hipótese.
📢Clique para ver mais:
- P-valor: Exercícios Resolvidos;
- Tabela de Distribuição Normal;
- Testes de Hipótese e de Aderência: Aulão Salva-Vidas.
Como Calcular o p-valor
A gente viu um monte de definição formal, mas e na prática, como a gente calcula o valor de p?! Bora ver um exemplo pra ficar mais claro!
Uma emissora de TV afirma que
Vamos colocar à prova a afirmação da emissora, isto é,
Beleza, observando a amostra de
Num primeiro momento, considere
1º Passo: Calcular a Estatística de Teste.
Nesse exemplo específico, o nosso parâmetro é a proporção, e por isso vamos usar usaremos a fórmula do
Nossa proporção amostral vai ser:
Logo, ficamos com o seguinte:
Guarda esse valor aí e vem comigo pro próximo passo! Ou então você também pode conferir o restante dessa resolução em vídeo! 😉 👇
2ª Passo: Calcular o p-valor.
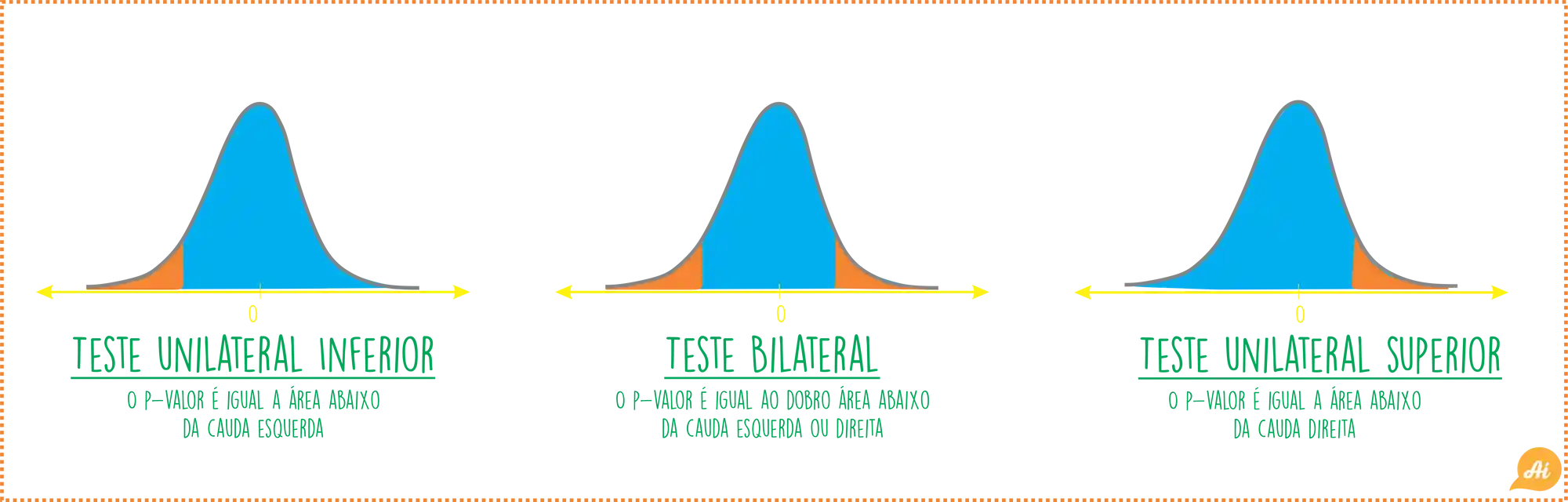
Nosso p-valor vai depender do tipo de teste que a gente faz. A gente vai fazer primeiro pro caso do exemplo, que é o unilateral inferior. Mas a ideia é a mesma para os casos bilateral e unilateral superior! Olha essa figura aqui:
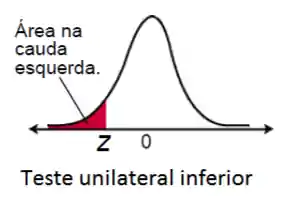
Essa área na cauda esquerda vai ser o p-valor. Esse
Então o que a gente tem que achar é essa área:
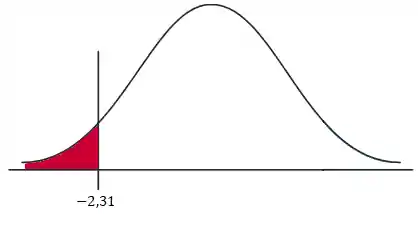
Como que a gente acha essa área? Isso mesmo, olhando na tabela da normal-padrão!
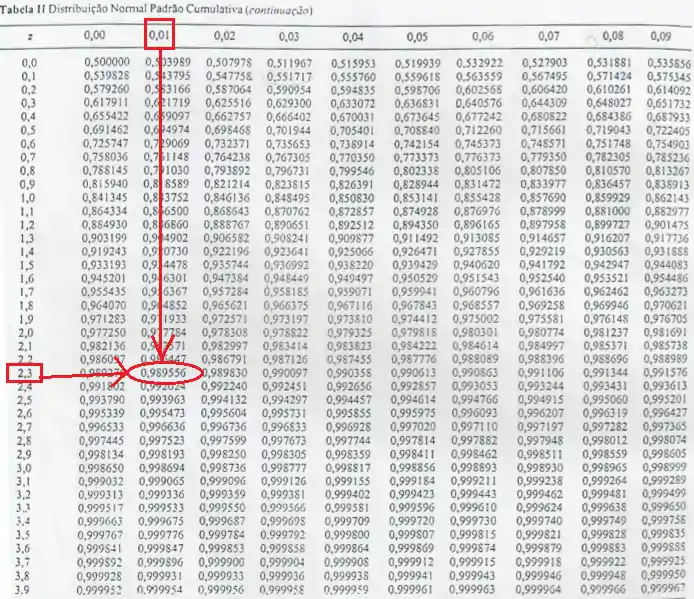
Então temos:
3º Passo: Tomar a decisão
O critério pra tomarmos a decisão aqui vai ser o seguinte:
Ou seja, vamos comparar o p-valor com o nível de significância, nosso querido
No nosso exemplo, temos um nível de significância
Logo nosso p-valor é menor! Dessa forma, rejeitamos nossa hipótese nula, o que nos leva a conclusão de que a proporção de televisores era menor que
Pra você entender o que aconteceu: o p-valor é uma medida de quanta evidência você tem contra a hipótese nula: ele representa a probabilidade de você obter um resultado tão extremo quanto o valor do
Outra forma de definir o p-valor é dizer que ele é o menor nível de significância para o qual a gente rejeita a hipótese nula. No nosso caso, ao nível de significância de
Teste Bilateral
Para o caso bilateral, a gente faria o mesmo procedimento, mas calcularia uma área como a da figura acima (cauda esquerda cauda direita). A única diferença seria essa conta da área, que a gente faz pela tabela!
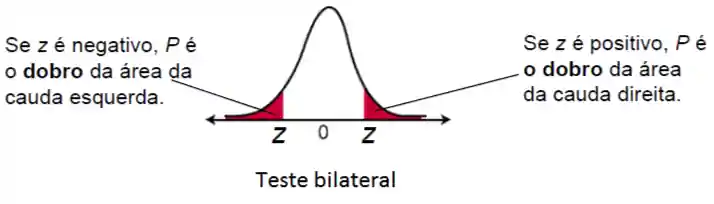
Teste Unilateral Superior
Seguindo a mesma lógica, no caso unilateral superior a gente calcula a área da cauda direita.
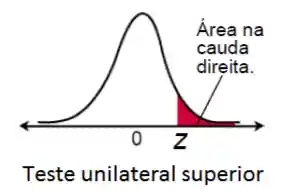
Agora vamos praticar com exercícios!
Teste Bilateral
Teste Unilateral Superior
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 211.
Um produto químico tem seu teor de pureza distribuído conforme uma Normal com média 0,72 e desvio padrão 0,02. A fim de aumentar a pureza, o produto é submetido a um tratamento. Dezesseis unidades amostrais do produto são selecionadas de forma aleatória e submetidas a esse tratamento. Em seguida, a pureza de cada unidade é determinada obtendo-se, para elas, uma média aritmética de 0,73. Podemos dizer que o tratamento contribui para o aumento da pureza?
- Qual seria a sua conclusão, ao nível de significância de 5%?
- Qual o p-valor?
Passo 1
(a)
Tá vamos lá, seguir o passo a passo que a gente aprendeu.
Definição das hipóteses:
Concorda? O que nos coloca no segundo caso lá que a gente viu.
Temos também que , e .
Passo 2
Próximo passo, estatística de teste:
Já que é um teste para média populacional.
Lembrando que tem distribuição Normal, podemos usar a tabela.
Passo 3
Para especificar a região de rejeição do teste, a gente sabe que esse caso é o caso2 da nossa teoria e que pra ele a região de rejeição é:
Usando a tabela:
Passo 4
Agora fazemos que:
A região de rejeição então será e a de aceitação .
Com isso, como o valor observado foi 0,73 devemos rejeitar a hipótese .
Passo 5
(b)
Temos que achar o valor limite ali onde a decisão passa de aceitação para rejeição de ou o contrário, como preferir. Isso acontece quando o valor observado é maior do que 0,73 que é a informação de .
Padronizando:
Usando aqueles paranauês lá:
Resposta
Exercício Resolvido #2
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 384.
As especificações dos pentes de memória RAM para computadores fabricados pela Companhia Boa Memória indicam que a porcentagem de pentes defeituosos não excede 5%. Uma amostra de cem desses pentes apresentou sete defeituosos.
Com base nesse resultado, podemos afirmar que as especificações estão incorretas?
- Qual a decisão a ser tomada, ao nível de significância de 0,01?
- Qual o nível crítico do teste?
Passo 1
(a)
Primeiros definimos as hipóteses:
Com isso já temos como dados:
E a proporção amostral de defeituosos é:
Passo 2
Nossa estatística de teste é:
Vamos calcular o que falta então, nosso ponto crítico:
Pra isso, só usei a tabela da Normal.
Isso quer dizer, como estamos num teste unilateral superior, que qualquer valor ACIMA desse cai na região crítica.
Com isso, como nossa estatística de teste não é maior que nosso ponto crítico, não rejeitamos a hipótese nula, pois estamos na região de aceitação!
Passo 3
(b)
O nível crítico do teste, ou o p-valor é:
O que é beeem maior que nosso nível de significância, então, mais uma vez, não podemos rejeitar a hipótese nula!
Resposta
Exercício Resolvido #3
P2- 2012.2 – UFRJ Teste de Hipóteses
Um estudo com 420.095 dinamarqueses usuários de telefones celulares descobriu que 135 deles tinham desenvolvido câncer no cérebro. Uma pesquisa anterior a essa, diz que a taxa de incidência de tipo de câncer era de 0,034% para pessoas que não usavam telefones celulares.
(b) Você diria que os usuários de telefone celular parecem ter uma taxa de incidência de câncer no cérebro diferente da taxa de incidência deste tipo de câncer em pessoas que não usam telefone celular? Realize um teste de hipóteses, adotando um nível de significância de 1% para dar a sua resposta.
(c) Calcule o -valor do teste realizado no item anterior.
Passo 1
(b)
Para esse teste, de acordo com o enunciado, a gente teria as hipóteses:
Pra esse caso a gente tem duas regiões de rejeição possível, vê la direitin no conteúdo:
E...
Passo 2
Substituindo os valores, as regiões de rejeição seriam..
A região de rejeição é então:
Passo 3
(c)
Vamos calcular o p-valor..
Substituindo todos os valores que a gente usou até agora no problema...
Usando aqueles paranauês que você já deve tá cansado de fazer..
Resposta
Exercício Resolvido #4
Elaboração Própria
Um médico quer testar um novo medicamento e seu efeito no tempo de resposta de outras substâncias. Para isso, ele tratou 100 ratos com o medicamento e injetou outra substância neles posteriormente, verificando o tempo de resposta. A literatura diz que a média do tempo de resposta dessa substância é de . O médico obtém uma média amostral de e desvio padrão de para o tempo de resposta nos ratos que está estudando. Você acha que o novo medicamento cumpriu seu objetivo? Teste a um nível de confiança de .
Passo 1
Primeiro construímos as hipóteses:
É menor por que queremos testar se o medicamento diminui o tempo de resposta mesmo!
Passo 2
Calculando nossa estatística de teste para a média:
Passo 3
Agora calculamos o p-valor e comparmos o valor dele com o nível de significância.
No teste unilateral inferior o p-valor é dado por:
Nosso nível de significância é , então:
E quando caímos nesse caso, nós rejeitamos a hipótese nula!
Resposta
Rejeita-se .
Exercício Resolvido #5
Lista de Exercício de Intervalo de Confiança e Teste de Hipóteses, Monitora Juliana, UFPR
O tempo para transmitir em determinada rede de computadores varia segundo um modelo normal, com médiae variância . Depois de algumas mudanças na rede acredita-se numa redução no tempo de transmissão de dados, além de uma possível alteração na variabilidade. Foram realizados 10 ensaios independentes com um arquivo de e foram anotados os tempos de transmissão, em segundos:
Existe evidência suficiente de que o tempo médio de transmissão foi reduzido? Use nível de significância de 1%.
Passo 1
Primeiro construímos as hipóteses:
É menor por que queremos testar se o tempo foi reduzido!
Passo 2
O enunciado nos menciona uma possível alteração na variabilidade, então vamos ter que ignorar essa variância populacional dada e calcular uma variância amostral a partir dos dados da amostra. Começando pela média amostral:
E a variância:
Então o desvio padrão amostral é:
Calculando nossa estatística de teste para a média com desconhecido:
Passo 3
Agora calculamos o p-valor e comparmos o valor dele com o nível de significância.
No teste unilateral inferior o p-valor é dado por:
Esse aí achamos indo na linha do grau de liberdade , que é o de nosso interesse , e procurando o valor mais próximo de . Achado o valor, vemos qual o corresponde na primeira linha da tabela!
Nosso nível de significância é , então:
E quando caímos nesse caso, nós rejeitamos a hipótese nula!
Resposta
Rejeita-se .