Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Covariância

Ver Todos os Exercícios

Teoria

Fala aí! Seja muito bem vindo ao Responde Aí! Bora aprender Covariância e Correlação de uma vez por todas?!

O que é Covariância?

A Covariância é uma medida estatística que serve pra a gente comparar duas variáveis aleatórias, medindo a dependência linear entre elas!

-Como assim? 😖

Por exemplo, imagina que você quer relacionar quantos horas de sono uma criança dorme, de acordo com a sua idade:

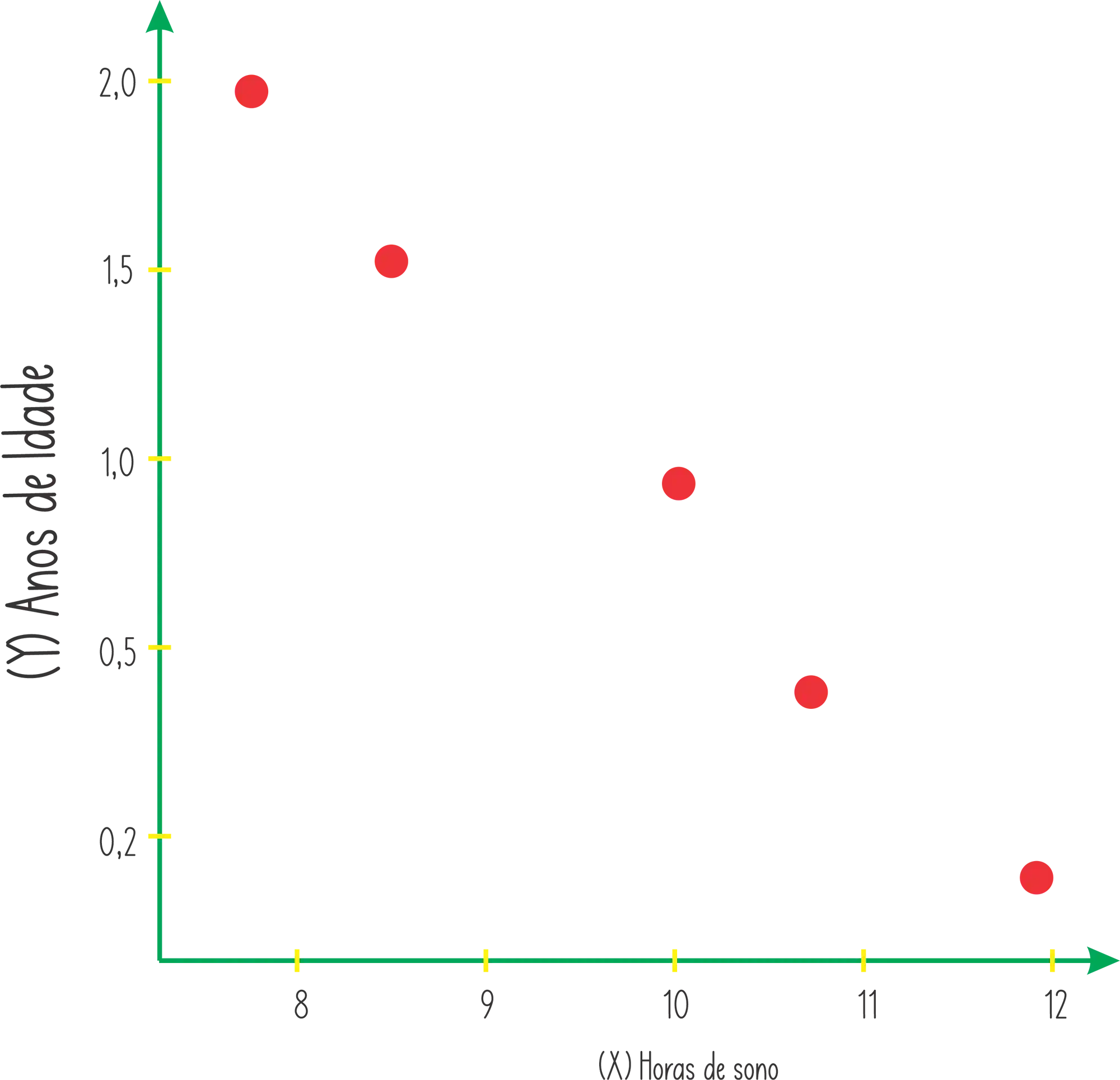
Gráfico com covariância negativa
Gráfico com covariância negativa

Olhando o gráfico a gente pode perceber que existe uma relação linear entre e , mas ela é inversamente proporcional, afinal quanto mais velha a criança, menos ela dorme. Nesse caso vamos ter uma covariância menor do que zero .

Agora e se a gente saber quantas horas um estudante passa estudando, de acordo com a sua idade? Se liga no gráfico abaixo:

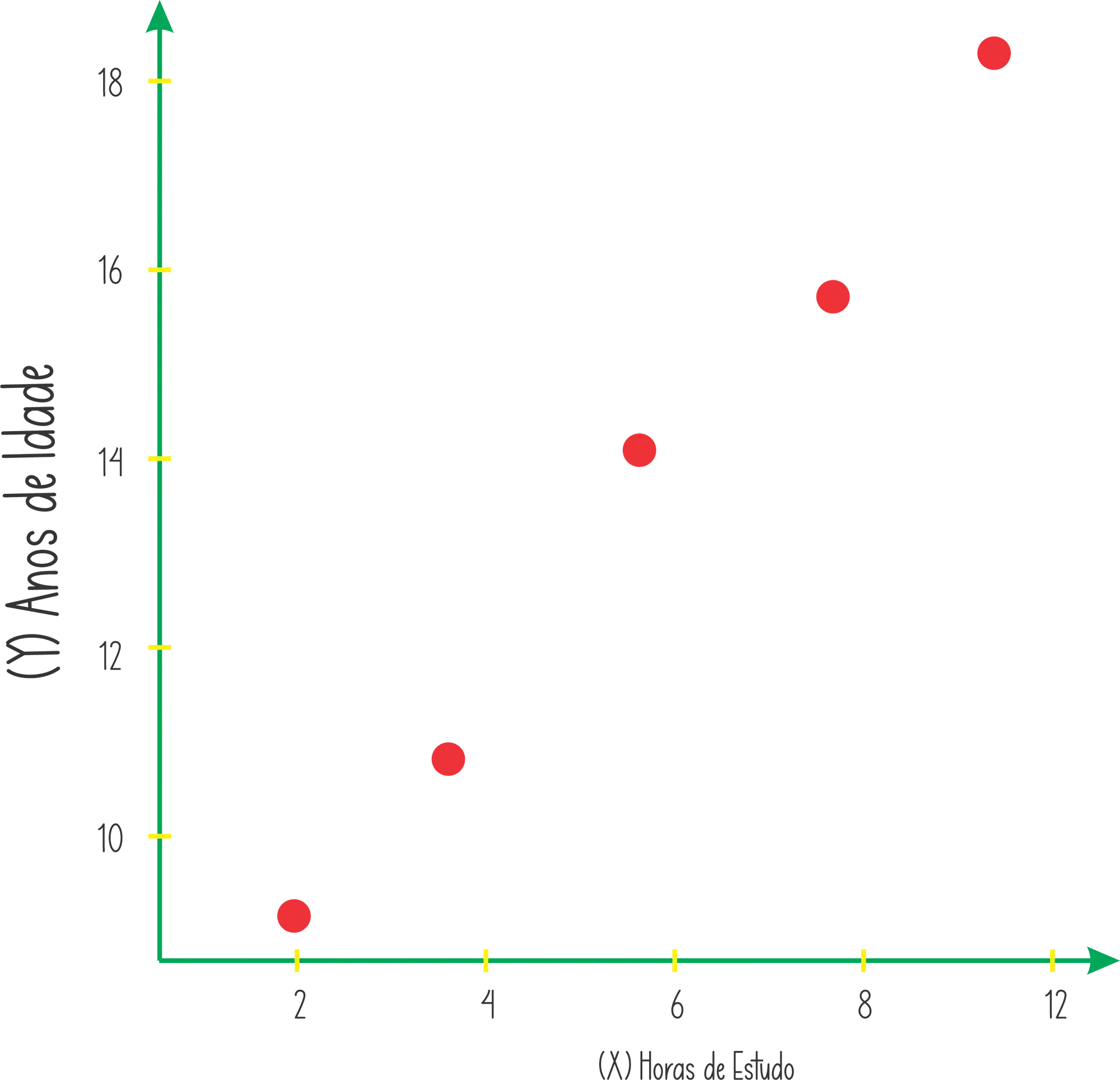
Gráfico com covariância positiva
Gráfico com covariância positiva

De novo vemos uma relação linear, mas agora quanto mais velho o estudante é, mais tempo ele passa estudando. Então teremos uma covariância entre e maior do que zero !

E agora pra encerrar, se eu te pergunto a relação entre a frequência que uma pessoa vai ao cinema com a sua altura! Você vai achar que eu estou doida 🤣🤣🤣

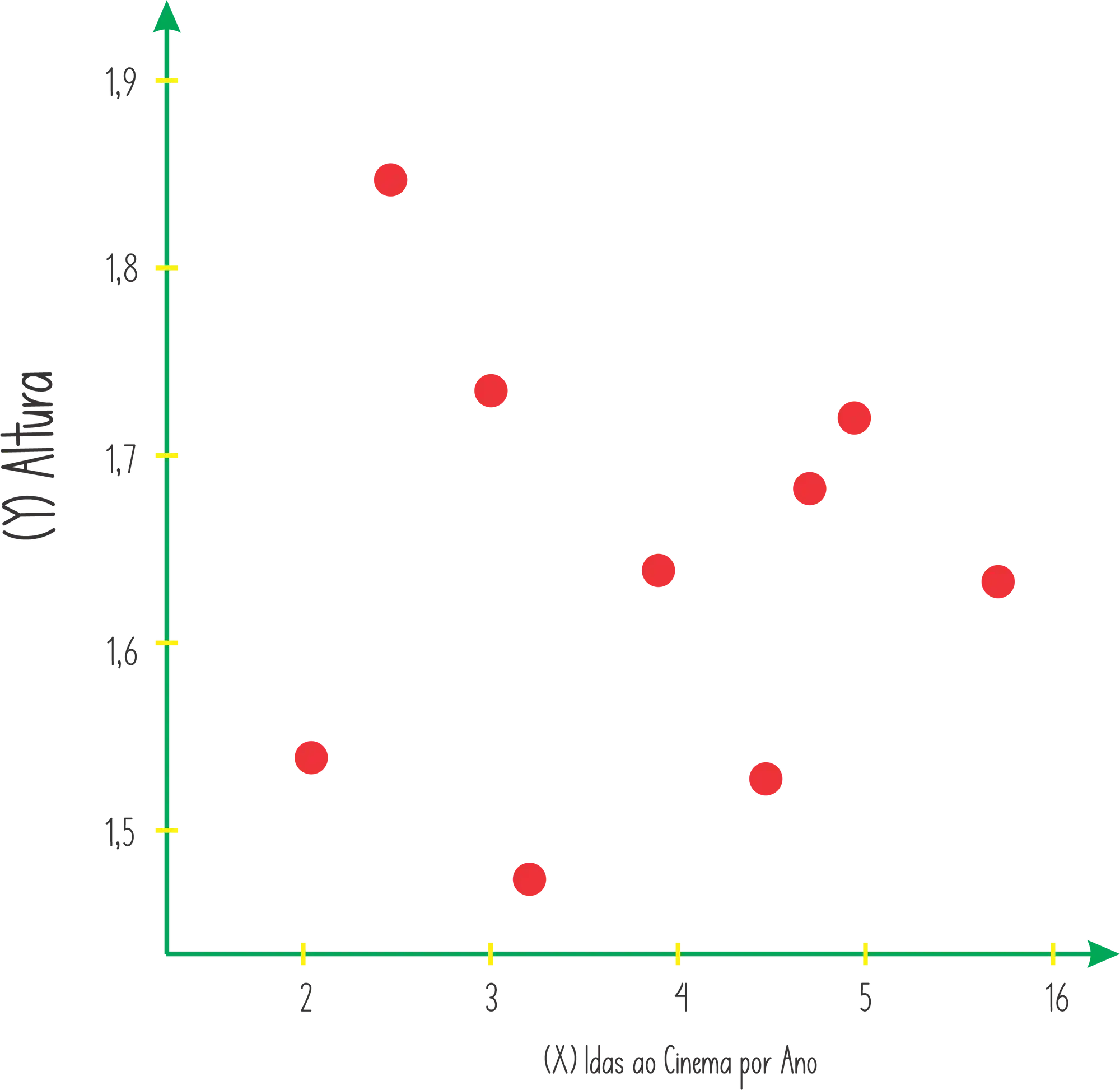
Gráfico com covariância inexistente
Gráfico com covariância inexistente

A gente pode ver no gráfico acima que realmente, uma coisa não tem nenhuma relação com a outra! Nesse caso, dizemos que as variáveis são independentes e sua covariância vai ser próxima, ou igual a zero!

Como Calcular a Covariância?

A gente pode calcular a covariância tanto quando estamos lidando com variáveis aleatórias discretas quanto continuas!

Nesse vídeo abaixo a gente te explica tudinho sobre como podemos fazer esses cálculos e como interpretar seus resultados. Dá uma conferida! 👇

Para calcularmos a covariância de duas variáveis aleatórias discretas, temos duas possibilidades! Na primeira usamos os valores esperados , também chamados de esperanças. Assim:

Fórmula da covariância a partir das esperanças
Fórmula da covariância a partir das esperanças

Ou então usamos as variâncias :

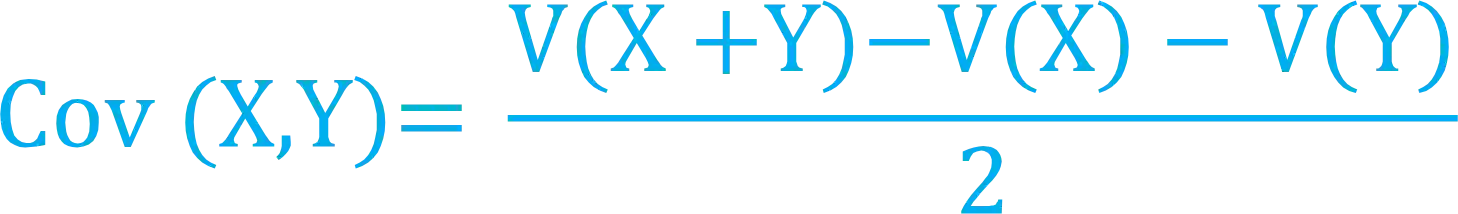
Fórmula da covariância a partir das variâncias
Fórmula da covariância a partir das variâncias

E quando estamos falando de variáveis aleatórias contínuas, usamos outra fórmula para calcular sua covariância:

Fórmula da covariância para v.a. contínuas
Fórmula da covariância para v.a. contínuas

Coeficiente de Correlação

O coeficiente de correlação é outro parâmetro que também serve para medir a interdependência das duas variáveis. Ele mede o grau de correlação linear entre as variáveis e pode ser calculado usando a seguinte fórmula:

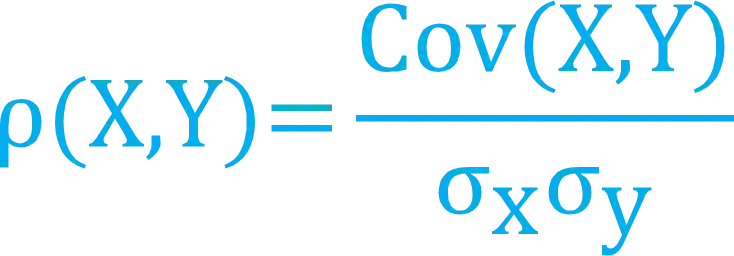
Coeficiente de correlação
Coeficiente de correlação

Onde e são os desvios padrões das variáveis e respectivamente. O coeficiente de correlação vai variar sempre entre e , onde:

  • Quando o coeficiente de correlação for igual a : Existe uma correlação linear inversamente proporcional entre as variáveis e
  • Quando o coeficiente de correlação for igual a : Existe uma correlação linear diretamente proporcional entre as variáveis e
  • Quando o coeficiente de correlação for igual a : As variáveis e são independentes.

Agora, vamos praticar com exercícios?

Coeficiente de Correlação

Exercícios Resolvidos

Exercício Resolvido #1

PUCRIO-P2-2013.2-1c)

b) Mostre que o coeficiente de correlação ρ ( X , Y ) é igual a 1 quando Y = a X + b e a > 0 .

Passo 1

A gente sabe que a fórmula do coeficiente de correlação é:

ρ X , Y = C o v X , Y V a r X . V a r Y

O que que a gente sabe mais?

C o v X , Y = E X Y - E X . E ( Y )

Substituindo Y = a X + b .

C o v X , Y = E X . a X + b - E X . E a X + b

Passo 2

Abrindo isso...

= E a X 2 + b X - E X E a X + E b

Aplicando as propriedades da esperança...

= a E X 2 + b E X - a E X 2 - b E X

= a E X 2 - a E X 2

= a E X 2 - E X 2

Aí você tem que ter a maldade de enxergar que o que tá ali dentro é a variância, lembra?

= a . V a r ( X )

Passo 3

Agora vamos pensar no denominador...

V a r X . V a r Y = V a r X . V a r a X + b

Aplicando as propriedades da variância.

= V a r X . a ² V a r ( X )

= a 2 . V a r X 2

= a . V a r ( X )

Passo 4

Voltando e substituindo na fórmula do coeficiente de correlação, temos:

ρ X , Y = a . V a r X a . V a r X = 1

Pronto, provamos o que a gente queria...

Dica, pessoal adora repetir essa questão em prova, vale a pena garantir esses pontos.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 216 - 17

O exemplo a seguir ilustra que ρ = 0 não implica independência. Suponha que (X,Y) tenha distribuição conjunta dada pela tabela abaixo.

a) Mostre que E(XY)=E(X)E(Y), donde ρ = 0

b) Justifique por que X e Y não são independentes.

Passo 1

a) Mostre que E(XY)=E(X)E(Y), donde ρ = 0

Sabemos que E X Y = ∑ x i y j P ( x = x i , y = y j )

Então

E X Y = - 1 - 1 1 8 + - 1 0 1 8 + - 1 1 1 8 + 0 1 1 8 + 0 0 0 + 0 1 1 8 + 1 - 1 1 8 + 1 0 1 8 + 1 1 1 8

E X Y = 0

Passo 2

Vamos calcular agora E(X) e E(Y):

E X = - 1 1 8 + 0 1 8 + 1 1 8 = 0

E Y = - 1 1 8 + 0 1 8 + 1 1 8 = 0

Assim

E X E Y = 0

Passo 3

Comparando, temos

E X Y = E X E Y = 0

Como querímos demonstrar.

Passo 4

b) Justifique por que X e Y não são independentes.

Uma forma de verificar se X e são independentes ou não é verificando se

P X = x i , Y = y j = P X = X i × P ( Y = y j )

Temos que testar TODAS as possibilidades. Se apenas uma não for válida podemos dizer que elas não são independentes. Pela tabela fica beeem mais tranquila a visualização.

Vamos direto no P X = 0 , Y = 0 , pois este vale 0 então é alta a chance de ele falhar.

P X = 0 = 1 8 + 0 + 1 8 = 2 8

P Y = 0 = 1 8 + 0 + 1 8 = 2 8

P X = 0 , Y = 0 = 2 8   . 2 8 = 4 64

Como P X = 0 , Y = 0 ≠ P X = 0 . P Y = 0 podemos afirmar que X e Y não são independentes.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

UFRJ-P1-2012.1-5(b)

Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja X a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja Y a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.

  1. Obtenha a distribuição conjunta de X   e Y através de uma tabela e diga se X   e Y são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de X   e de Y . Em seguida, obtenha P X = 0 ; Y = 1 e P ( X = 2 ; Y = 0 ) . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
  2. Calcule a covariância de X   e Y .

Passo 1

(a)

A gente tem que montar nossa tabela marota.

Primeiro vamos entender melhor o problema.

X : n ú m e r o   d e   b o l a s   b r a n c a s   r e t i r a d a s   n a s   d u a s   e x t r a ç õ e s

X pode assumir os valores: 0(se não sair nenhuma branca nas duas), 1 ou 2.

Y : 1   ,                         s e   a   p r i m e i r a   b o l a   é   b r a n c a 0   ,               s e   a   p r i m e i r a   b o l a   é   v e r m e l h a

Bom, vamos seguir os conselhos do exercício.

Passo 2

Vamos começar com as distribuições marginais.

Começando por Y .

P Y = 0 = 2 5

Já que são 2 bolas vermelhas, num total de 5 bolas.

P Y = 1 = 3 5

Já que são 3 bolas brancas, num total de 5 bolas.

Passo 3

Agora vamos fazer a distribuição marginal de X .

P X = 0 = 2 5 × 1 4 = 1 10

Já que pra não sair nenhuma bola branca, na primeira retirada tem que sair uma vermelha, 2 / 5 , e na segunda também tem que sair uma vermelha, 1 / 4 (lembrando que é sem reposição).

P X = 1 = 3 5 × 2 4 + 2 5 × 3 4 = 6 10 = 3 5

Pra sair no total 1 branca, temos duas opções: sair branca na primeira (3/5) e vermelha na segunda (2/4) ooou sair vermelha na primeira (2/5) e branca na segunda (3/4).

Pra finalizar.

P X = 2 = 3 5 × 2 4 = 3 10

Pra sair 2 brancas, tem que sair uma branca na primeira (3/5) e uma branca na segunda (2/4).

Passo 4

Seguindo os conselhos do exercício, vamos calcular agora:

P X = 0 ; Y = 1 =   ?

Probabilidade de sair bola branca na primeira retirada e no total não sair nenhuma branca. HAM? Impossível, concorda?

Então:

P X = 0 ; Y = 1 = 0

Agora calcular, P X = 2 ; Y = 0 =   ?

Também é impossível, certo? Não dá pra sair duas bolas brancas se na primeira retirada sair uma vermelha. Então:

P X = 2 ; Y = 0 = 0

Passo 5

Vamos montar a tabela com os valores que a gente já tem.

Completando a tabela, lembrando que o somatório das linhas e das colunas tem que ser igual aos valores da distribuição marginal, a gente ficará com:

Pronto, era isso que a gente queria.

Passo 6

Agora pra ver se são independentes é ver se existe algum caso que não verifique a seguinte afirmação.

P X = x i , Y = y i = P ( X = x i ) × P ( Y = y i )

Nesses casos é bom olhar pra exemplos que tenham 0 na tabela, fica mais tranquilo verificar. Por exemplo:

P X = 2 , Y = 0 = 0

P X = 2 × P Y = 0 = 3 10 × 2 5

Então,

P ( X = 2 , Y = 0 ) ≠ P ( X = 2 ) × P ( Y = 0 )

E com isso dizemos que X e Y não são independentes.

Passo 7

(b)

Pra calcular a covariância, vamos usar a fórmula.

C o v X , Y = E X , Y - E X × E Y

E X = 0 × 1 10 + 1 × 3 5 + 2 × 3 10 = 6 5

E Y = 0 × 2 5 + 1 × 3 5 = 3 5

E X , Y = 1 × 1 × 3 10 + 1 × 2 × 3 10 = 9 10

Substituindo na fórmula.

C o v X , Y = 9 10 - 6 5 × 3 5

C o v X , Y = 9 50

Resposta

a   n ã o   s ã o   i n d e p e n d e n t e s

b 9 50

Exercício Resolvido #4

UFRJ-P1-2012.2-4

Considerando a população dos profissionais à busca de emprego em uma certa fatia do mercado de trabalho, há duas habilidades consideradas importantes para se ter sucesso: dominar o Inglês e dominar a Informática. Sabe-se que:

  1. a proporção de profissionais que dominam o Inglês é igual a proporção de profissionais que dominam a Informática (denote por p   essa proporção comum às duas habilidades);
  2. o número médio de habilidades por profissional é 1,4;
  3. a variância desse número de habilidades por profissional é 0,24.

Calcule:

  1. o valor de   p ;
  2. o coeficiente de correlação ρ   entre dominar o Inglês e dominar a Informática
  3. a proporção q   de profissionais que possuem ao mesmo tempo as duas habilidades.

Sugestão: Defina as variáveis aleatórias.

Passo 1

(a)

Vamos determinar nossas variáveis assim:

X : 1 ,               s e   o   p r o f i s s i o n a l   d o m i n a   i n g l ê s 0 ,                               c a s o   c o n t r á r i o                                                      

Y : 1 ,               s e   o   p r o f i s s i o n a l   d o m i n a   i n f o r m á t i c a 0 ,                                                         c a s o   c o n t r á r i o                                                      

E:

X + Y = número de habilidades que o profissional possui

Passo 2

Os dados dos problemas nos dizem que:

  • proporção dos que dominam inglês é igual aos que dominam informática e é p .

    • P X = 1 = P Y = 1 = p

  • número médio de habilidades é igual a 1,4.

    • E X + Y = 1,4

  • variância do número de habilidades é 0,24

Var X + Y = 0,24

Passo 3

Se:

E X + Y = E X + E Y = 1,4

E como X e Y seguem uma distribuição de Bernoulli, onde só temos possibilidades de sucesso (1) e de fracasso (0).

E X = E Y = p

Var X = Var Y = p ( 1 - p )

Então:

p + p = 1,4

p = 0,7

E:

Var X = Var Y = 0,7 × 1 - 0,7 = 0,21

Passo 4

(b)

O coeficiente de correlação é dado pela fórmula:

ρ x y = Cov X , Y σ x ⋅ σ y

Como:

Var   X = Var Y = 0,21

σ x = σ y = 0,21

Passo 5

Um dos jeitos de calcular Cov ( X , Y ) é:

Var X + Y = Var X + Var Y + 2 ⋅ Cov X , Y

Pelo problema a gente sabe:

Var X + Y = 0,24

Var X = V a r Y = 0,21

Então:

Cov X , Y = 0,24 - 0,21 - 0,21 2

Cov X , Y = - 0,09

Passo 6

Substituindo tudo na fórmula agora:

ρ x y = - 0,09 0,21

ρ x y = - 3 7

Passo 7

(c)

Agora é marotagem, se liga.

Vou chamar de X Y uma nova variável, onde:

X Y = 1 ,       s e   X = 1   e   Y = 1   0 ,       c a s o   c o n t r á r i o        

Ou seja, só tem sucesso, quando o profissional domina inglês e informática ao mesmo tempo. A gente sabe de acordo com o enunciado que a probabilidade disso acontecer é:

p = q

E que desse jeito, X Y também seguirá uma distribuição de Bernoulli, com E X Y = q .

Passo 8

Se usarmos a fórmula que aprendemos:

E X Y = Cov X , Y + E X ⋅ E Y

Podemos determinar o valor de q .

q = - 0,09 + 0,7 × 0,7

q = 0,4

Resposta

a   p = 0,7

b   ρ x y = - 3 7

c   q = 0,4

Exercícios de Livros Relacionados

A variável aleatória X tem uma distribuição de probabilidades: f X ( x ) = x 8 ,0 ≤ x ≤ 4 Encontre a distribuição de probabilidades de Y=(X-2)^2
Mostre que se X 1 , X 2 , X 3 , . . . , X p forem variáveis aleatoriamente independentes e Y = c 1 X 1 + c 2 X 2 + c 3 X 3 + . . . + c p X p V ( Y ) = c 2 1 V ( X 1 ) + c 2 2 V ( X 2 ) + . . . + c 2 p
Considere a situação do Problema 10 do Capítulo 6. Verifique se E(XY) = E(X) E(Y). O que você pode concluir?
Considere a situação do Problema 10 do Capítulo 6. Verifique se X e Y são independentes.
Suponha que X tenha uma distribuição de probabilidades uniformes f X ( x ) = 1 ,1 ≤ x ≤ 2 Encontre a distribuição de probabilidades da variável aleatória Y=e^x