Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Medidas de Dispersão para V.A. Multidimensionais

Ver Todos os Exercícios

Teoria

Medidas de Dispersão de uma V.a. Multidimensional Discreta

Agora vamos ver como ficam aqueles valores que a gente conhece pra v.a. pra variáveis bidimensionais. Relaxa aí que são muitas fórmulas, não precisa se assustar, nossa tabelinha vai ajudar muito.

Por exemplo na tabela abaixo onde relacionamos o número X de defeitos de uma pessoa com o número Y de qualidades:

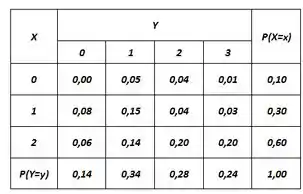
E ( X ) e E ( Y ) continuam sendo calculadas da mesma forma.

A gente iria ter:

E X = 0 × 0,1 + 1 × 0,3 + 2 × 0,6 = 1,5

E Y = 0 × 0,14 + 1 × 0,34 + 2 × 0,28 + 3 × 0,24 = 1,62

Mas aí surgirá E X , Y → esperança da variável bidimensional, que será calculada assim:

E X , Y = 0 × 0 × 0,00 + 0 × 1 × 0,05 + 0 × 2 × 0,04 + 0 × 3 × 0,01 + 1 × 0 × 0,08 +

1 × 1 × 0,15 + 1 × 2 × 0,04 + … + 2 × 3 × 0,20 = 2,6

Pegou ? Dá uma olhada na nossa tabela de novo pra você pegar bem o raciocínio. Fui multiplicando todos os valores x i e y i pelos valores de dentro da tabela.

Sabendo isso, você está preparado para ser apresentado a mais fórmulas

Covariância → C o v ( X , Y ) . Existem 2 fórmulas possíveis.

C o v X , Y = E X , Y - E X . E ( Y )

V a r X + Y = V a r X + V a r Y + 2 . C o v ( X , Y )

Nota: Se X e Y são independentes então C o v X , Y = 0

Medidas de Dispersão de uma V.a. Multidimensional Contínua

Pra fechar, adivinha? Faltou aprender a calcular a esperança e a variância dessas variáveis bidimensionais contínuas.

E X = ∫ - ∞ ∞ ∫ - ∞ ∞ x . f x , y   d x d y

E Y = ∫ - ∞ ∞ ∫ - ∞ ∞ y . f x , y   d x d y

V a r X = ∫ - ∞ ∞ ∫ - ∞ ∞ x 2 . f x , y   d x d y - E X 2

V a r Y = ∫ - ∞ ∞ ∫ - ∞ ∞ y 2 . f x , y   d x d y - E Y 2

E a esperança bidimensional contínua vai ser:

E X Y = ∫ - ∞ ∞ ∫ - ∞ ∞ x y . f x , y   d x d y

Reparou que lá no caso discreto a gente denotou a esperança bidimensional como E X , Y e agora como E ( X Y ) ? Pois é, isso não faz diferença! Só fica mais claro para a gente diferenciar o caso discreto do contínuo. Fica tranquilo(a) que significam a mesma coisa.

Lembrando que o desvio padrão ainda é a raiz quadrada a variância, nada mudou!

Existem também fórmulas para esperança condicional e variância condicional.

A esperança condicional acontece sempre que for pedido “qual a esperança de Y , dado que X = x ...”:

E Y X = x = ∫ - ∞ ∞ y . f y x   d y

Então precisamos conhecer nossa função de densidade condicional para calculá-la, que vimos no tópico passado!

E a variância condicional quando for pedido a variância de Y , dado que X = x :

V a r Y X = x = E Y 2 X = x - E Y X = x 2

Repara que a variância condicional segue o mesmo padrão de todas as fórmulas de variância que vimos! É a esperança da variável ao quadrado menos a esperança ao quadrado dessa mesma variável. Mas como estamos no caso condicional, as esperanças da equação passam a ser as condicionais também!

O que mudou, é que agora vou te apresentar duas novas medidas, ansioso? Haha, nada demais!

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 206-03

Considere a distribuição conjunta de X e Y, conhecida, dada na tabela abaixo.

Considerando X e Y independentes.

b) Calcule as médias de X, Y e XY

d) Calcule a variância de X,Y e X+Y

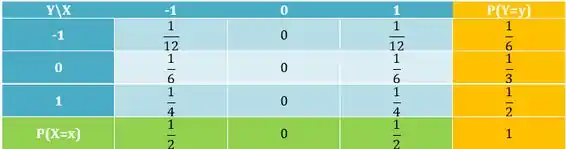
Passo 1

Sabemos que

E X = ∑ x . P ( X = x )

Portanto

E X = ∑ i = - 1 1 x i . P X = x i = - 1 . 1 2 + 0 . 0 + 1 . 1 2 = 0

E Y = ∑ j = - 1 1 y j . P Y = y j = - 1 . 1 6 + 0 . 1 3 + 1 . 1 2 = 1 3

Passo 2

Para calcular E(XY) usaremos

E X Y = ∑ x i y j P ( X = x i , Y = y j )

E X Y = - 1 - 1 1 12 + - 1 0 0 + - 1 1 1 12 + 0 - 1 1 6 + 0 0 0 + 0 1 1 6 + 1 - 1 1 4 + 1 0 0 + 1 1 1 4 = 0

Passo 3

Para o cálculo da Var(X) precisamos lembrar da seguinte fórmula:

V a r X = E X 2 - E X 2

Portanto precisamos calcular E ( X 2 )

E X 2 = - 1 2 1 2 + 0 2 0 + 1 2 1 2 = 1

E Y 2 = - 1 2 1 6 + 0 2 1 3 + 1 2 1 2 = 2 3

Substituindo na fórmula teremos

V a r X = 1 - 0 2 = 1

V a r Y = 2 3 - 1 3 2 = 5 9

Passo 4

Para calcular Var(X+Y) usaremos

V a r X + Y = V a r X + V a r Y + 2 . C o v ( X , Y )

C o v X , Y = E X , Y - E X . E ( Y )

Vamos lá!

C o v X , Y = 0 - 0.1 3 = 0

V a r X + Y = 1 + 5 9 + 2 × 0 = 14 9

Resposta

E X = 0

E Y = 1 3

E X Y = 0

V a r X = 1

V a r Y = 5 9

V a r X + Y = 14 9

Exercício Resolvido #2

FONTE -08

Numa urna têm-se cinco bolas marcadas com os seguintes números: -1, 0, 0, 0, 1. Retiram-se três bolas, simultaneamente: X indica a soma dos números extraídos e Y o maior valor da trinca. Calcule:

b) E(X) e Var(X)

c) E(X,Y)

Passo 1

Montamos a tabela de distribuição em um exercício anterior lembram? (Exercício de Fixação 2 – Tipo Introdução à Probabilidade Conjunta):

Y\X

-1

0

1

P(Y=y)

0

0,3

0,1

0

0,4

1

0

0,3

0,3

0,6

P(X=x)

0,3

0,4

0,3

Vamos calcular agora E(X)

E X = ∑ x . P X = x

E X = - 1 . 0,3 + 0 0,4 + 1 0,3 = 0

Passo 2

Calculando Var(X)

V a r X = E X 2 - E X 2

Para isso precisamos calcular E X 2

E X 2 = - 1 2 0,3 + 0 2 0,4 + 1 2 0,3 = 0,6

Portanto

V a r X = 0,6 - 0 2 = 0,6  

Passo 3

Agora precisamos calcular E(XY). Pela tabela é fácil, saca só:

E X , Y = 0 - 1 0,3 + 0 0 0,1 + 0 1 0 + 1 - 1 0 + 1 0 0,3 + 1 1 0,3 = 0,3

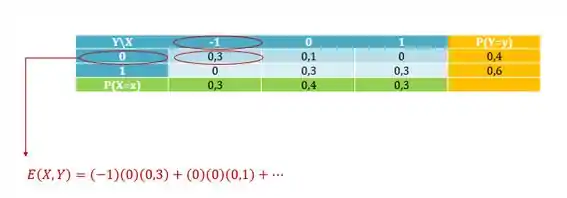
Resposta

E X = 0

V a r X = 0,6

E X , Y = 0,3

Exercício Resolvido #3

PUCRIO-P2-2014.2-5

Seja " X " e " Y " duas variáveis aleatórias contínuas, das quais se conhece:

f x , y = x . y 3 + x 2   ,     o n d e   0 < x ≤ 1   e   0 ≤ y ≤ 2

f x ( x ) = x 2 + 2 . x 3       ,     o n d e   0 < x ≤ 1

f y y = 1 3 + y 6       ,     o n d e   0 ≤ y ≤ 2

Pede-se:

  1. Calcule a média condicional de X dado Y = y . Se y = 1,3 , qual a média condicional de X dado Y = 1,3 ?
  2. Calcule a variância condicional de X dado Y = y . Se y = 1,3 , qual a variância condicional de X dado Y = 1,3 ?

Passo 1

(a)

Para calcular a condicional de X , dado Y = y , usaremos a fórmula:

f X | Y x y = f x , y f y y

Já conhecemos tudo:

f x , y = x . y 3 + x 2

f y y = 1 3 + y 6

Então, substituindo:

f X | Y x y = x . y 3 + x 2 1 3 + y 6

f X | Y x y = 3 x 2 + x y 3 2 + y 6

f X | Y x y = 3 x 2 + x y 3 × 6 2 + y

f X | Y x y = 6 x 2 + 2 x y 2 + y

Passo 2

Agora para calcular a média condicional de X , dado Y = y , usamos:

E X Y = y = ∫ 0 1 x . f X | Y x y   d x

Note que a integral vai de 0 a 1 pois é o intervalo em que vale a variável x . Assim:

E X Y = y = ∫ 0 1 x . 6 x 2 + 2 x y 2 + y   d x

= 1 2 + y . ∫ 0 1 6 x 3 + 2 x 2 y   d x

= 1 2 + y . 6 x 4 4 + 2 y x 3 3 0 1

= 1 2 + y × 3 2 + 2 y 3

= 1 2 + y × 9 + 4 y 6

= 9 + 4 y 12 + 6 y

Passo 3

Pra calcular a média condicional com Y = 1,3 é só substituir ali em cima y = 1,3 .

Ficaria...

E X Y = 1,3 = 9 + 4 × 1,3 12 + 6 × 1,3

= 0,717

Passo 4

(b)

Pra calcular a variância condicional de X , dado Y = y , vamos usar primeiro a relação:

V a r X Y = y = E X 2 Y = y - E X Y = y 2

Então primeiro temos que calcular E X 2 Y = y .

E X 2 Y = y = ∫ 0 1 x ² . f x y   d x

Note a integral de 0 a 1 novamente aqui!

= ∫ 0 1 x ² . 6 x 2 + 2 x y 2 + y   d x

= 1 2 + y . ∫ 0 1 6 x 4 + 2 x 3 y   d x

= 1 2 + y . 6 x 5 5 + 2 y x 4 4 0 1

= 1 2 + y × 6 5 + 2 y 4

= 1 2 + y × 24 + 10 y 20

= 24 + 10 y 40 + 20 y

Dividindo tudo por 2:

E X 2 Y = y = 12 + 5 y 20 + 10 y

Passo 5

Mas calculamos lá em cima que

E X Y = y = 9 + 4 y 12 + 6 y

Certo? Substituindo, então, os valores que a gente agora já conhece.

V a r X Y = y = E X 2 Y = y - E X Y = y 2

V a r X Y = y = 12 + 5 y 20 + 10 y - 9 + 4 y 12 + 6 y 2

= 12 + 5 y 10 ( 2 + y ) - 9 + 4 y 6 ( 2 + y ) 2

= 12 + 5 y 10 ( 2 + y ) - 9 + 4 y 2 36 2 + y 2

O mmc dos denominadores é 180 2 + y 2 , então vamos escrever as duas frações com um denominador comum:

= 18 ( 12 + 5 y ) ( 2 + y ) 180 2 + y 2 - 5 9 + 4 y 2 180 2 + y 2

= 18 ( 5 y 2 + 22 y + 24 ) 180 2 + y 2 - 5 ( 16 y 2 + 72 y + 81 ) 180 2 + y 2

= 90 y 2 + 396 y + 432 - ( 80 y 2 + 360 y + 405 ) 180 2 + y 2

= 10 y 2 + 36 y + 27 180 2 + y 2

Ou então:

= 10 y 2 + 36 y + 27 180 ( y 2 + 4 y + 4 )

= 10 y 2 + 36 y + 27 180 y 2 + 720 y + 720

Portanto:

V a r X Y = y = 10 y 2 + 36 y + 27 180 y 2 + 720 y + 720

Passo 6

Agora pra calcular isso pra Y = 1,3 , é só substituir o valor:

V a r X Y = 1,3 = 10 × 1,3 2 + 36 × 1,3 + 27 180 × 1,3 2 + 720 × 1,3 + 720

= 90,7 1960,2 ≅ 0,046

Resposta

a   0,717

b   0,046

Exercício Resolvido #4

PUCRIO-P2-2013.2-5

Sejam X e Y v.a. contínuas com densidade conjunta:

f x , y = - 3 4 y + 2 x y       ,     o n d e   0 ≤ x ≤ 2   e   0 ≤ y ≤ 1

Dados:

Marginal de X : f x = x - 1 2

Marginal de Y : f y = 4 y - 3 2 y

Pede-se:

  1. Densidade condicional de Y dado X = x .
  2. Média condicional de Y   dado X = x , e calcule o valor quando x = 1,5 .
  3. Variância condicional de Y   dado X = x , e calcule o valor quando x = 1,5 .

Passo 1

(a)

Pra resolver cada um desses itens vai ser basicamente aplicar fórmula, então vamos lá.

Pra calcular a densidade condicional f Y X = x , vamos aplicar:

f Y X = x = f x , y f x

Os dois já são dados do problema, só fazer conta.

Passo 2

Vamos as contas...

= - 3 4 y + 2 x y x - 1 2

= - 3 4 y + 2 x y 2 x - 1 2

= 2 × - 3 4 y + 2 x y 2 x - 1

= - 6 4 y + 4 x y 2 x - 1  

= - 6 y + 16 x y 4 2 x - 1

= - 3 y + 8 x y 2 2 x - 1  

= - 3 y + 8 x y 4 x - 2

Tá bom por aí já.

Passo 3

(b)

Agora a fórmula é:

E Y X = x = ∫ 0 1 y . f ( Y | X = x )   d y

De 0 a 1 porque esses são os limites de y do enunciado.

Esse valor de dentro da integral foi o que a gente usou no item anterior.

= ∫ 0 1 y . - 3 y + 8 x y 4 x - 2   d y

= 1 4 x - 2 ∫ 0 1 - 3 y 3 2 + 8 x y ² d y

Passo 4

Vamos integrar...

∫ 0 1 - 3 y 3 2 + 8 x y 2 d y =

= - 3 × 2 5 y 5 2 + 8 x 3 y 3 0 1

= - 6 5 + 8 x 3

E Y X = x = - 6 5 + 8 x 3 4 x - 2

Não pode esquecer desse denominador aí que eu tinha tirado da integral. Vou simplificar.

= - 3 × 6 + 5 × 8 x 15 4 x - 2

= - 18 + 40 x 60 x - 30

= 20 x - 9 30 x - 15

Passo 5

Agora podemos calcular pra quando x = 1,5 .

E Y X = 1,5 = 20 × 1,5 - 9 30 × 1,5 - 15

= 0,7

Passo 6

(c)

A fórmula vai ser:

V a r Y X = x = E Y 2 X = x - E Y X = x 2

Guarda isso.. vamos fazer parte por parte... o segundo valor ali que a gente precisa, a gente tem do item anterior. Vamos calcular então pela fórmula, o primeiro.

E Y 2 X = x = ∫ 0 1 y ² . f Y X = x d y

Bem parecido com o item anterior, só que é ao quadrado ali...

Fica assim:

= ∫ 0 1 y ² . - 3 y + 8 x y 4 x - 2   d y

Passo 7

Vamos resolver a integral...

= ∫ 0 1 y ² . - 3 y + 8 x y 4 x - 2   d y

= 1 4 x - 2 . ∫ 0 1 - 3 y 5 2 + 8 x y 3   d y

Vamos guardar essa parte de fora e focar na integral...

= - 3 × 2 7 y 7 2 + 8 x 4 y 4 0 1

= - 6 7 + 2 x

= - 6 + 14 x 7

Juntando tudo:

= - 6 + 14 x 7 4 x - 2

= - 6 + 14 x 28 x - 14

Simplificando por dois..

E Y 2 X = x = 7 x - 3 14 x - 7

Passo 8

Agora joga tudo naquela primeira fórmula lá:

V a r Y X = x = E Y 2 X = x - E Y X = x 2

V a r Y X = x = 7 x - 3 14 x - 7 - 20 x - 9 30 x - 15 2

Vou fazer uma parada pros denominadores ficarem iguais... vou dividir toda a galera da primeira parte por 14 e geral da segunda por 30 .

= 1 2 x - 3 14 x - 1 2 - 2 3 x - 3 10 x - 1 2 2

Agora fica melhor de simplificar, porque fica mais fácil juntar as coisas..

= 1 2 x - 3 14 × x - 1 2 - 2 3 x - 3 10 2 x - 1 2 2

Abrindo tudo...

= 1 2 x 2 - 3 14 x - 1 4 x + 3 28 - 4 9 x 2 + 4 10 x - 9 100 x 2 - x + 1 4

= 0,056 x 2 - 0,064 x + 0,017 x 2 - x + 0,25

É isso aí.

Passo 9

Pra fechar só substituir x = 1,5 nesse monstro aí.

= 0,047

Resposta

a   - 3 y + 8 x y 4 x - 2

b   20 x - 9 30 x - 15       ,     0,7

c   0,056 x 2 - 0,064 x + 0,017 x 2 - x + 0,25     ,     0,047

Exercícios de Livros Relacionados

Numa sala estão cinco crianças cujas idades são (em anos): 3, 3, 4, 5, 5. Escolhem-se três crianças ao acaso para formar uma trinca. X indica a idade da mais nova da turma, e Y à da mais velha. Calcul
Suponha que X seja uma variável aleatória contínua com distribuição de probabilidades f X ( x ) = x 18 ,0 ≤ x ≤ 6 Encontre a distribuição de probabilidades da variável aleatória Y=2X+10Encontre o valo
Considere que os pesos de indivíduos sejam independentes e normalmente distribuídos, com uma média de 160 libras e um desvio padrão de 30 libras. Suponha que 25 pessoas se espremam em um elevador proj
Suponha que X seja uma variável aleatória com distribuição de probabilidade f X ( X ) = 1 4 para 1,2,3,4Encontre a distribuição de probabilidade de Y=2X+1
Uma variável aleatória X tem a seguinte distribuição de probabilidades: f X ( x ) = e - x , x ≥ 0 Encontre a distribuição de probabilidades para Y=X^2Encontre a distribuição de probabilidades para Y=X