Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distribuição Uniforme

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos aprender um pouquinho sobre distribuição uniforme.

Uma distribuição uniforme é um tipo de distribuição de probabilidades contínua. Esse nome chique serve só pra dizer que existe um número de resultados dentro de um espaço amostral e todos com a mesma probabilidade de acontecer. Bora ver um pouquinho mais a fundo e colocar um pouco mais de sentido nisso aí? Vem comigo.

Ah, se você preferir, pode assistir esse videozinho aqui, com o assunto bem explicadinho pra você 😉

Distribuição Uniforme Contínua

Vamos focar um pouquinho mais na distribuição uniforme para variáveis contínuas. Então se você não tá dominando bem esse tipo de variável ainda, dá uma conferida nessa página aqui que tem tudo bem explicadinho.

Beleza, quando eu falo que uma variável aleatória segue uma distribuição uniforme contínua em um intervalo , isso quer dizer que tem a mesma probabilidade de assumir qualquer valor contínuo entre e . Só com essa informação a gente já conseguiria encontrar uma função para descrever a probabilidade da nossa variável assumir um valor dentro do intervalo. Consegue ver como?

Função Densidade de Probabilidade

Dá só uma olhada nesse gráfico: no eixo , vou colocar o intervalo de valores que a variável aleatória contínua pode assumir, e no eixo vai ficar a probabilidade dela assumir cada valor.

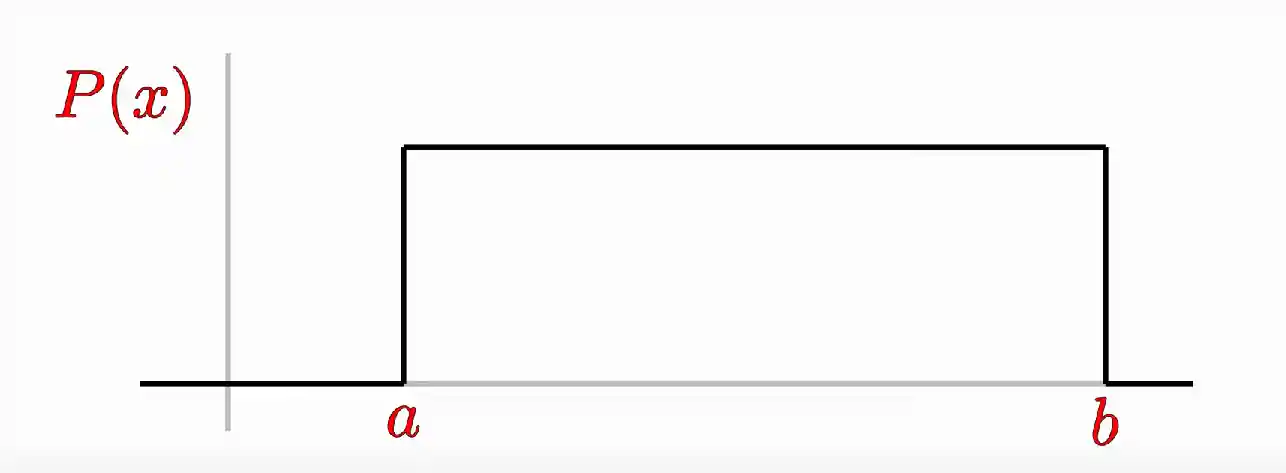
Gráfico de uma distribuição uniforme.
Gráfico de uma distribuição uniforme.

Consegue ver como cada valor de ali dentro daquele intervalo tem o mesmo correspondente em , ou seja, a mesma probabilidade? Como a gente faz pra achar essa probabilidade?

Bom, concorda comigo que se somarmos a probabilidade da nossa variável assumir todo e cada valor possível, o resultado disso vai ser igual a 1? Matematicamente, escrevemos isso assim:

Não para por aí. Quando a gente faz essa soma, estamos também encontrando a área abaixo daquele gráfico ali. Em uma distribuição de probabilidade contínua, a gente teria que calcular a integral de e aplicar os limites de integração.

Mas como aqui estamos falando de uma distribuição uniforme, a figura desse gráfico é um retângulo. E neste caso, podemos também encontrar a área multiplicando sua base pela altura, concorda?

E qual a base desse retângulo? É .

E a altura? A altura vai ser o próprio , que é aquilo que queremos encontrar!

Aí é só a gente dividir os dois lados por e encontramos a probabilidade da nossa função assumir cada valor.

A partir disso aí que encontramos, você consegue encontrar a probabilidade do nosso se encontrar dentro de qualquer subintervalo pertencente a . Quer ver só? Se liga nesse exemplo:

Exemplo: O ônibus que você pega para o trabalho se atrasa uniformemente de 2 a 10 minutos. Se ele se atrasar mais do que 7 minutos, você chegará atrasado ao trabalho. Qual a probabilidade de você chegar atrasado?

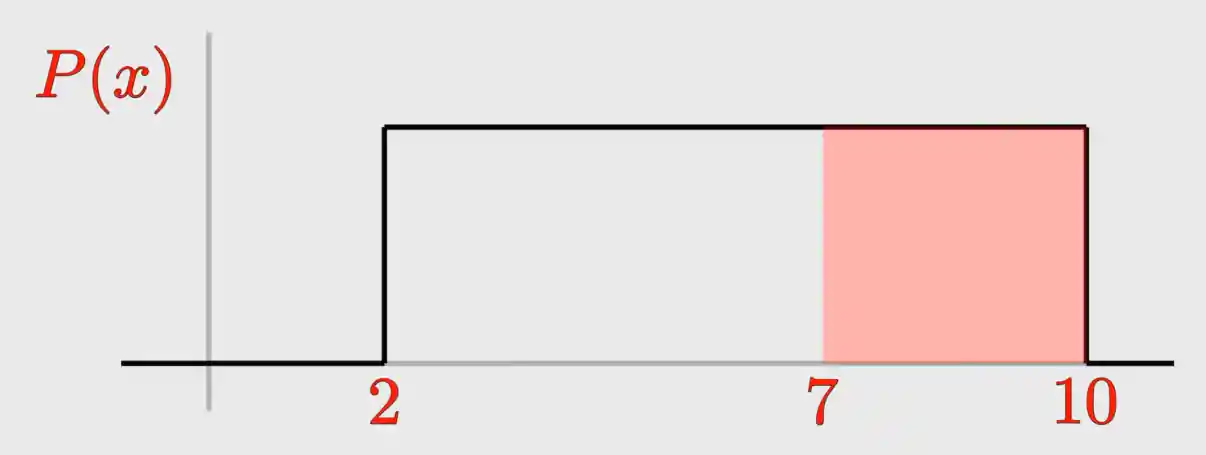
Vamos fazer uma interpretação gráfica igual fizemos agora há pouco. Olha só, nosso intervalo total de possíveis valores de é , mas só nos interessa aqueles valores com .

Podemos prosseguir com o cálculo da área daquele retângulo menor destacado ali para encontrarmos a probabilidade que nos interessa.

Qual a base do retângulo? É .

E a altura? Como já descobrimos, é .

Tá aí a resposta que queríamos!

Esperança e Variância

Em alguns exemplos você também vai ser cobrado acerca desses termos aqui. A esperança, como o nome sugere, é aquele valor que podemos esperar que a variável aleatória assuma, e ele é dado nada mais, nada menos, do que pela média do intervalo.

A variância é um pouquinho menos intuitiva, então vou pedir só pra você lembrar dessa fórmula, beleza?

Bora praticar com mais alguns exercícios e ficarmos mais craques ainda!

Esperança e Variância

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-P1-2014.2.-3A

Por saber que há uma grande procura por imóveis em determinada região muito valorizada, uma construtora decide comprar um terreno e construir uma casa nesse local.

  1. Uma parte dos recursos necessários para isso será obtida através de um financiamento. Especialmente, admita que o percentual do gasto total a ser financiado se comporta como uma variável aleatória com distribuição Uniforme entre 40 % e 70 % . Qual é o coeficiente de variação dessa variável?

Passo 1

(a)

Temos uma v.a. que representa o gasto total a ser financiado que segue uma distribuição Uniforme entre 40 e 70 .

X   ~   U 40 ; 70

E vamos calcular o coeficiente de variação que é o desvio padrão dividido pela média:

c v = σ E X

Passo 2

Pra calcular a média e o desvio padrão de uma distribuição uniforme é só lembrar das fórmulas.

E X = a + b 2 = 40 + 70 2

E X = 55

Passo 3

O desvio padrão é a raiz quadrada da variância que é:

V a r X = b - a 2 12 = 70 - 40 2 12

V a r X = 75

O desvio padrão vai ser:

σ = 75

Passo 4

Juntar tudo pra ter o coeficiente de variação:

c v = 75 55

c v ≅ 0,157

Resposta

a ≅ 0,157

Exercício Resolvido #2

PUCRIO-P2-2013.1-3

Seja X uma variável aleatória contínua com densidade Uniforme no intervalo de - θ , + θ .

Em cada caso abaixo calcule " θ " de forma a satisfazer a condição dada.

  1. P X > 1 2 = 1 4
  2. P X < 1 4 = 3 4
  3. P X > 1 2 = 2 . P X < - 1
  4. P X < 1 2 = 2 . P X > 1 4

Passo 1

Estamos tratando de uma v.a. com densidade Uniforme, vamos primeiro recapitular qual a função de densidade da v.a. Uniforme.

f x = 1 b - a   ,                   s e   a ≤ x ≤ b           0   ,                                 c a s o   c o n t r á r i o

Porém, pra calcular as probabilidades, vamos usar a função acumulada FDA, que é:

F x = 0   ,                   s e   x ≤ a x - a b - a   ,                   s e   a ≤ x ≤ b 1   ,                     s e     x ≥ b

Nessa questão, como o intervalo é - θ , + θ , vamos ter que:

a = - θ

b = θ

Aí vamos ter:

F x = x + θ 2 θ

Beleza?

Passo 2

(a)

P X > 1 2 = 1 4

P X > 1 2 = 1 - P X < 1 2

Usando a FDA, é só substituir x = 1 2 .

= 1 - 1 2 + θ 2 θ

Isso tem que ser igual a 1 4 .

1 - 1 2 + θ 2 θ = 1 4

Passo 3

Matemática... mudando as coisas de lado...

1 2 + θ 2 θ = 3 4

1 2 + θ = 3 2 . θ

θ - 3 2 θ = - 1 2

- 1 2 θ = - 1 2

θ = 1

Passo 4

(b)

P X < 1 4 = 3 4

É só aplicar direto a FDA.

P X < 1 4 = 1 4 + θ 2 θ = 3 4

1 4 + θ = 3 2 θ

θ - 3 2 θ = - 1 4

- 1 2 θ = - 1 4

θ = 1 2

Passo 5

(c)

P X > 1 2 = 2 . P X < - 1

Partes por partes...

P X > 1 2 = 1 - P X < 1 2

= 1 - 1 2 + θ 2 θ

E:

P X < - 1 = - 1 + θ 2 θ

Agora é só juntar tudo numa equação e resolver.

Passo 6

P X > 1 2 = 2 . P X < - 1

1 - 1 2 + θ 2 θ = 2 . - 1 + θ 2 θ

Cortando o 2   ali.

1 - 1 2 + θ 2 θ = - 1 + θ θ

Vou multiplicar geral por 2 θ .

2 θ - 1 2 + θ = - 2 + 2 θ

Corta o 2 θ dos dois lados...

- 1 2 - θ = - 2

θ = - 1 2 + 2

θ = 3 2

Passo 7

(d)

P X < 1 2 = 2 . P X > 1 4

Mesma coisa, uma de cada vez.

P X < 1 2 = 1 2 + θ 2 θ

P X > 1 4 = 1 - 1 4 + θ 2 θ

Joga na equação e resolve.

Passo 8

1 2 + θ 2 θ = 2 . 1 - 1 4 + θ 2 θ

1 2 + θ 2 θ = 2 - 1 4 + θ θ

Multiplicar todo mundo por 2 θ de novo.

1 2 + θ = 4 θ - 1 2 + 2 θ

1 2 + θ = 4 θ - 1 2 - 2 θ

1 2 + θ = 2 θ - 1 2

θ = 1

Resposta

a   θ = 1

b   θ = 1 2

c   θ = 3 2

d   θ = 1

Exercício Resolvido #3

CEFET-LISTA VA- REGINA-7

A espessura de um semicondutor, está uniformemente distribuída entre 0,2050 μ m e 0,2150 μ m (micrômetros).

  1. Determine a função de distribuição acumulada da espessura do semicondutor.
  2. Determine a proporção de semicondutores que excedem 0,2125 μ m em sua espessura.
  3. Que espessura é excedida por 10% dos semicondutores?

Passo 1

(a)

Sabemos que a espessura está uniformemente distribuída.

X   ~   U 0,2050 ; 0,2150

A gente sabe que a função de distribuição tem a cara:

F x = 0   ,                   s e   x ≤ a x - a b - a   ,                   s e   a ≤ x ≤ b 1   ,                     s e     x ≥ b

Substituindo os valores de a e b :

F x = 0   ,                   s e   x ≤ 0,2050 x - 0,2050 0,01   ,                   s e   0,2050 ≤ x ≤ 0,2150 1   ,                     s e     x ≥ 0,2150

F x = 0       ,                   s e   x ≤ 0,2050 100 x - 20,5   ,                   s e   0,2050 ≤ x ≤ 0,2150 1         ,                     s e     x ≥ 0,2150

Passo 2

Para calcular então   P ( X > 0,2150 ) , basta a gente fazer:

P 0,2125 < X < 0,2150 = 0,2150 - 0,2125 0,01

Esse 0,01 aí é exatamente a amplitude total → 0,2150 - 0,2050 = 0,01 .

= 0,0025 0,01

= 0,25

Passo 3

(c)

Temos que:

P X > k = 0,1

Onde k é a espessura excedida por 10% dos semicondutores.

Resolvendo:

P k < X < 0,2150 = 0,1

0,2150 - k 0,01 = 0,1

0,2150 - k = 0,001

k = 0,2140

Resposta

a   F x = 0       ,                   s e   x ≤ 0,2050 100 x - 20,5   ,                   s e   0,2050 ≤ x ≤ 0,2150 1         ,                     s e     x ≥ 0,2150

b   0,25

c   0,2140

Exercício Resolvido #4

UFF – Departamento de Estatística, Apostila profª Ana Maria Lima de Farias

Você está interessado em dar um lance em um leilão de um lote de terra. Você sabe que existe um outro licitante. Pelas regras estabelecidas para este leilão, o lance mais alto acima de R $   100.000,00 será aceito. Suponha que o lance do seu competidor seja uma variável aleatória uniformemente distribuída entre R $   100.000,00 e R $   150.000,00 .

  1. Se você der uma lance de R $   120.000,00 , qual é a probabilidade de você ficar com o lote?

Passo 1

a)

X : v a l o r   d o   l a n c e   d o   c o m p e t i d o r

O enunciado nos diz que:

X ~ U ( 100000 ; 150000 )

Sabemos que a função de densidade de uma distribuição uniforme é dada por

f x = 1 b - a ,     s e   a < x < b 0 ,       c a s o   c o n t r á r i o

Onde a , b é o nosso intervalo [ 100.000,150.000 ] . Então no nosso caso f ( x ) fica:

f x = 1 50000 ,     s e   100000 < x < 150000 0 ,       c a s o   c o n t r á r i o

E a probabilidade pedida é de com um lance de R $ 120000 nós ganharmos do competidor, ou seja, o lance X dele deve ser menor que isso:

P ( 1000000 < X < 120000 )

Podemos calcular essa probabilidade integrando a função de densidade:

P X < 120.000 = ∫ - ∞ 120000 1 50000 d x = ∫ 100000 120000 1 50000 d x = x 50000 100000 120000 = 0,4

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

UFF – Departamento de Estatística, Apostila da profª Ana Maria Lima de Farias

O rótulo de uma lata de coca-cola indica que o conteúdo é de 350   m l . Suponha que a linha de produção encha as latas de forma que o conteúdo seja uniformemente distribuído no intervalo [ 345 , 355 ] .

O controle de qualidade aceita uma lata com conteúdo dentro de 4   m l do conteúdo exibido na lata. Qual é a proporção de latas rejeitadas nessa linha de produção?

Passo 1

O controle de qualidade aceita latas que estejam dentro do intervalo de ( 350 ∓ 4 ) m l , ou seja, [ 346,354 ] .

Para saber a proporção de latas rejeitadas, temos que saber a proporção de latas que o controle de qualidade rejeita, ou seja, a proporção de latas fora desse intervalo. Denotando o conteúdo de uma lata por X :

P s e r   r e j e i t a d a = P X < 346 + P ( X > 354 )

Porque X deve ser menor que 346 m l O U maior que 354 m l , e O U em probabilidade nós somamos duas probabilidades. Vamos calcular cada uma delas então.

Nossa função de densidade é:

f x = 1 b - a ,       s e   a < x < b 0 ,     c a s o   c o n t r á r i o

Onde a = 345 e b = 355 , então:

f x = 1 10 ,       s e   345 < x < 355 0 ,     c a s o   c o n t r á r i o

Passo 2

Então:

P X < 346 = ∫ - ∞ 346 1 10 d x = ∫ 345 346 1 10 d x =   ( 346 - 345 ) 10 = 0,1

E a outra:

P X > 354 = ∫ 354 + ∞ 1 10 d x = ∫ 354 355 1 10 d x = ( 355 - 354 ) 10 = 0,1

E chegamos em:

P s e r   r e j e i t a d a = P X < 346 + P X > 354 = 0,1 + 0,1 = 0,2

Resposta

0,2

Exercícios de Livros Relacionados

Erro de medida, que é distribuído contínua e uniformemente de -3 a +3 milivolts, é adicionado ao valor verdadeiro da tensão de um circuito. Então, a medida é arredondada para o milivolt mais próximo,
A espessura de um flange em um componente de espaçonave é uniformemente distribuída entre 0.95 e 1.05 milímetros.Determine a função de distribuição cumulativa da espessura do flange.Determine a propor
Suponha que a variável aleatória discreta X tome os valores 1, 2 e 3 com igual probabilidade. Ache a distribuição de probabilidade de Y = 2X + 3.
Com referência ao Ex. 4.10, calcule P(X = 2), se n = 4 e, para n arbitrário, verifique P(X = n-1) = P (exatamente uma tentativa mal sucedida) é igual a 1 n + 1 ∑ 1 i
Um experimento consiste em tentativas independentes. Deve-se admitir que por causa da "aprendizagem", a probabilidade de obter um resultado favorável cresça com o número de tentativas realizadas. Espe