Medidas de Centralidade e Dispersão para V.A. Contínua
Produzido por Jorge Alberto NascimentoTeoria
E(X), VaR(X)
Tratando agora de v.a. contínuas, teremos outras maneiras de calcular a esperança e a variância de .
- a esperança é calculada como:
- a variância será:
São basicamente fórmulas que você terá que gravar.

Para o caso do equipamento eletrônico... Calma aí, você lembra desse caso?
O tempo de vida útil de um equipamento eletrônico de determinado tipo pode ser expresso por uma v.a. contínua , cuja função de densidade é:
Então faremos:
![]()
Isso significa que o equipamento dura em média 2 anos.
E:
![]()
Calma, desculpa o momento bruxaria, é que a resolução teria integração por partes e você não precisa se preocupar com isso.
Ah! Cabe lembrar que continua sendo , nada mudou.
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 171-08
A v.a. contínua tem a f.d.p.
a) Se b for um número que satisfaz , calcule
b) Calcule e
Passo 1
a) Olha aí! Já queremos calcular uma condicional :O
Mas você lembra como é uma condicional? Vamos relembrar juntos?
Nesse caso ele quer . Vamos dar nome aos termos ok?
- Evento A:
- Evento B:
- Evento :
Assim
Passo 2
Vamos calcular cada um separadamente e depois juntar:
i)
Note que se está no intervalo , então também está, portanto podemos fazer esta integral normalmente.
Continuando a conta...
ii)
Como está novamente naquele intervalo faremos a integral normalmente. Só precisamos lembrar que como é um número negativo, é MAIOR que .
Finalmente vamos unir (i) e (ii):
Passo 3
b) Calcule e
Sabemos que
Substituindo teremos:
Passo 4
Para Var(X) utilizaremos a seguinte equação:
Como já temos precisamos agora encontrar :
Substituindo
Assim teremos que:
Resposta
a)
b)
Exercício Resolvido #2
UFF-1°VE-4
O tempo de reação (em segundos) a um determinado estímulo é uma variável aleatória contínua com fdp:
- Deduza e faça o gráfico.
- Qual é a probabilidade de o tempo de reação ser no máximo segundos?
- Entre e segundos?
- Calcule o tempo de reação esperado.
- Calcule o desvio padrão do tempo de reação.
Passo 1
(a)
Vamos usar:
Para :
Passo 2
(b)
Passo 3
(c)
Passo 4
(d)
O tempo de reação esperado nada mais é do que a esperança.
Passo 5
(e)
Para o desvio padrão, primeiro calculamos a variância e depois tiramos a raiz quadrada.
O desvio padrão será então:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
UFRJ-P1-2013.1-3
A distribuição da renda, expressa em salários mínimos (s.m.), dos membros de um sindicato é caracterizada pela função de densidade:
.
- Calcule o desvio padrão (em s.m.) dessa variável;
- Determine o nível salarial (em s.m.) abaixo do qual estão os salários de 87,5% (ou seja, ) desses profissionais.
Passo 1
(a)
Vamos começar calculando .
Passo 2
Calculamos também .
Passo 3
Agora já estamos aptos a calcular
E então calcular o que o exercício pede, .
Passo 4
(b)
A gente sabe que a FDA dessa variável pode ser expressa assim:
Corta o 3 ai na sua folha, hehe..
Passo 5
O que o exercício quer é que a gente diga pra qual valor de , vale 87,5%.
Resposta
Exercício Resolvido #4
UFRJ-PF-2014.1-2
Sabemos que a esperança e a variância de uma v.a. podem ser encaradas, respectivamente, como a abscissa do centro de gravidade e o momento de inércia de uma distribuição de massa, e que isso vale tanto no caso discreto como no caso contínuo. Admita que a função de densidade da v.a. contínua é dada por:
- Determine e Dica: Fazer um gráfico da função.
- Admita agora que é uma v.a. discreta que só pode assumir três valores: e . Obtenha a função de probabilidade da v.a. , sabendo que e Isso significa que ambas as distribuições de massa têm o mesmo centro de gravidade e o mesmo momento de inércia, embora uma seja contínua e a outra seja discreta.
Passo 1
(a)
Vamos só aplicar fórmulas de variáveis aleatórias contínuas...
Para a esperança:
Em todo o domínio da nossa função... isso nos dá:
Procura os semelhantes aí e vai cortando... viu o que sobra? Nada kkk
O exercício diz pra você desenhar a função por isso, desenhando você veria que ela é simétrica e daí poderia concluir que a esperança seria zero.
Passo 2
Para variância a gente usa a relação:
Sendo que a gente já sabe que , falta só calcular , que é:
Em todo o domínio da nossa função... isso nos dá:
E daí:
Passo 3
(b)
A gente conhece os três possíveis valores de , que são: .
Pra fazer a função de distribuição da variável falta só a gente determinar com que probabilidade cada um desses valores acontece, ou seja, a gente tem que determinar:
Show?
E a gente sabe o valor da esperança e da variância, que são iguais ao que a gente calculou em (a) pra .
Passo 4
A esperança de uma variável discreta, como que a gente faz? Lembra? A gente multiplica os possíveis valores da variável pelas suas probabilidades... então:
Daí:
Ok!
Passo 5
Vamos usar o dado da variância agora...
Como ...
E isso é:
Só que a gente sabe que ... daí:
Passo 6
Daí você se pergunta como que a gente faz pra descobrir se ele sempre tá zerando...
Lembra que o somatório de todas essas probabilidades de uma variável tem que dar ?
Então:
Show? Já temos a função de probabilidade de .
Resposta
Exercício Resolvido #5
UFRJ-PF-2014.2-1
A proporção de álcool em certo produto pode ser considerada uma variável aleatória com a seguinte função densidade de probabilidade:
- Calcule o valor esperado e a variância de .
- Suponha que o preço de venda do produto dependa da proporção de álcool. Se o produto é vendido por reais/l, caso contrário por reais/l. Expresse em função de e a distribuição de probabilidades do lucro líquido por litro de produto, supondo que o custo por litro é de reais.
Passo 1
(a)
Nesse item vamos basicamente aplicar umas fórmulas de variáveis aleatórias contínuas...
Para calcular o valor esperado (esperança), a gente usa:
Que vai ficar:
Passo 2
Para variância a gente usa:
Aí temos que calcular primeiro:
Passo 3
Juntando tudo:
Passo 4
(b)
Bom, se o produto é vendido por , caso contrário, é vendido por .
E o preço de produção é fixo e igual a
Então o nosso lucro, que vou chamar de , pode ter dois valores.
Dependendo do preço de venda.
Passo 5
Vamos calcular então a prob. de que será exatamente a prob. do lucro ser de .
Desisto, pega sua calculadora aí!
Passo 6
Se a probabilidade de é de ... quanto seria a probabilidade de isso não acontecer?
Sendo assim, a gente vai ter que o lucro vai ser:
E essa é a distribuição de prob. do lucro: seus possíveis valores e as probabilidades referentes a cada um deles.
Resposta
Exercício Resolvido #6
Morettin & Bussab, Estatística Básica 5ª edição, pág 171
Calcule a esperança, a variância e a f.d.a. da variável aleatória com a densidade triangular em .
Passo 1
Primeiro temos que entender como é a função triangular de a :
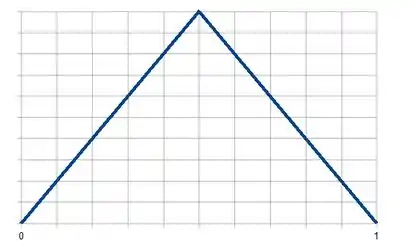
E pra valores fora desse intervalo, nossa função vale zero. E podemos considerar que esse aí é um triângulo isósceles, então o ponto médio da nossa função é na metade do intervalo, ou seja, . E repara comigo, até temos uma reta crescente, e depois desse ponto temos outra reta, agora decrescente. Temos que descrever essas duas retas como funções.
Passo 2
A gente sabe que a área de um triângulo é dada por , certo? E como esse triângulo é uma função de densidade, vamos igualar essa área a 1 para descobrir o valor de (o ponto máximo dessa função). Estamos fazendo isso porque a área nada mais é que uma integral! Então:
Mas sabemos que a base é nosso intervalo :
Então o ponto máximo da nossa função é . Agora podemos descobrir as equações para as nossas duas retas. Vamos começar pela crescente.
Ela corta o gráfico no ponto e , e como é uma reta, vai ter formato . Substituindo os pontos conhecidos obtemos o sistema:
Disso aí descobrimos que e . Então nossa equação fica
Agora vamos ver a segunda reta. Ela tem os pontos e . Temos então o sistema:
Isso dá pra gente que e . Então .
Juntando as duas retas, nossa função de densidade é dada por:
Passo 3
Agora podemos calcular a esperança, que é dada por:
E a variância é:
Calculando essa integral:
Resposta
Exercício Resolvido #7
UFF – Departamento de Estatística, Apostila da profª Ana Maria Lima de Farias
Uma variável aleatória tem função de distribuição acumulada dada por
Calcule e
Passo 1
Por essa expressão, sabemos que a função de densidade existe no intervalo de , certo? Então vamos fazer o contrário do que fizemos até agora, ou seja, vamos derivar para achar :
E sabemos que a esperança de uma v.a. contínua é dada por:
No nosso caso ficaria:
Passo 2
E a variância é dada por: