Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Propriedades da Variância

Ver Todos os Exercícios

Teoria

A Variância Amostral é uma medida de dispersão que nos diz o quanto os valores de um conjunto de dados estão distantes da média e elas tem algumas propriedades bem interessantes!

Bora conhecer as Propriedades da Variância?! 😍

📢 Clique para ver mais:

Esperança e variância de uma constante

Se é uma constante, então sua esperança também é uma constante e sua variância é igual a zero.

Linearidade da esperança

Seja uma variável aleatória independente, e , com e quaisquer reais. Então a sua esperança é dada pela seguinte relação linear:

Variância de

Sendo e reais a sua variância é dada por:

Desvio padrão de

Sendo e reais o seu desvio padrão é dado por:

Agora vamos ver como essas propriedades da variância são usadas em um exemplo!

Exemplo: Uma variável é descrita pela função . Sabendo que E , calcule a esperança, a variância e o desvio padrão de .

Passo 1: Aplicar a esperança dos dois lados da equação

Ou seja, fazemos:

Usando a propriedade da linearidade da esperança, temos:

Como :

Pronto, achamos a esperança!

Passo 2: Aplicar a variância dos dois lados da equação

Usando a propriedade da variância:

²

E como :

O desvio padrão é então:

Prontinho! Agora vamos praticar com exercícios?

Linearidade da esperança

Variância de

Desvio padrão de

Exemplo: Uma variável é descrita pela função . Sabendo que E , calcule a esperança, a variância e o desvio padrão de .

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,140-17

O tempo T, em minutos, necessário para um operário processar certa peça é uma v.a. com a seguinte distribuição de probabilidade

a) Calcule o tempo médio de processamento.

Para cada peça processada, o operário ganha um fixo de $2,00, mas, se ele processa a peça em menos de seis minutos, ganha $0,50 em cada minuto poupado. Por exemplo, se ele processa a peça em quatro minutos, recebe a quantia adicional de $1,00.

b) Encontre a distribuição, a média e a variância da v.a. G: quantia de $ ganha por peça.

Passo 1

a) Tempo médio de processamento

Quando ele fala de tempo médio → Está falando da média!

E T = 2 × 0,1 + 3 × 0,1 + 4 × 0,3 + 5 × 0,2 + 6 × 0,2 + 7 × 0,1 = 4,6

Passo 2

b) Encontre a distribuição, a média e a variância da v.a. G: quantia de $ ganha por peça.

Vamos analisar quem é a v.a. G

O quanto cada operário ganha é:

G = $ = 2,00 + 0,5 ( 6 - t )

Ou seja, são $2,00 fixos + $0,50 por minuto poupado.

Passo 3

Vamos substituir os t possíveis nesta equação para saber os valores possíveis de G:

- t = 2

G ( t = 2 ) = 2 + 0,5 . 6 - 2 = 2 + 0,5 × 4 = 4

- t = 3

G t = 3 = 2 + 0,5 6 - 3 = 2 + 0,5 × 3 = 3,5

- t = 4

G t = 4 = 2 + 0,5 6 - 4 = 2 + 0,5 × 2 = 3

- t = 5

G t = 5 = 2 + 0,5 6 - 5 = 2 + 0,5 × 1 = 2,5

- t = 6

G t = 6 = 2 + 0,5 6 - 6 = 2,0

Passo 4

Montando uma tabela de distribuição de G:

Passo 5

Calculando o que se pede:

E G = 2 × 0,3 + 2,5 × 0,2 + 3,0 × 0,3 + 3,5 × 0,1 + 4,0 × 0,1 = 2,75

V a r G = E G 2 - E G 2

E G 2 = 4 × 0,3 + 6,25 × 0,2 + 9 × 0,3 + 12,25 × 0,1 + 16 × 0,1 = 7,975

V a r G = 7,975 - 2,75 2 = 0,4125

Resposta

a) 4,6

b)E(G)=2,75 e Var(G)=0,4125

Exercício Resolvido #2

PUCRIO-P1-2014.1-1C

c) Seja “ X ” uma v.a. discreta com E X = 6 e D P X = 3 é o desvio padrão de X . Se Y = 2 3 . X - 9 , quem é E ( Y ) e D P ( Y ) .

Passo 1

A gente sabe o que?

E X = 6     e     D P X = 3

Beleza, e a gente quer calcular esses valores para a v.a. Y = 2 3 . X - 9 .

Pra isso a gente vai precisar só usar as propriedades da esperança e do desvio padrão. Lembra?

Passo 2

E Y = E a X + b = a . E X + b

E Y = E 2 3 . X - 9

= 2 3 E X - 9

Usamos a propriedade a multiplicação de uma constante e da esperança de uma constante.

= 2 3 . 6 - 9

= - 5                  

Passo 3

A mesma coisa pro desvio padrão:

D P a X + b = a . D P ( X )

D P Y = D P 2 3 . X - 9

= 2 3 . D P X

= 2 3 . 3 = 2          

Resposta

E Y = - 5

D P Y = 2

Exercício Resolvido #3

UERJ-lista 1 prof Fabiano-18(b)

Uma transportadora de cargas possui quatro caminhões de aluguel. O aluguel é realizado por dia e que a distribuição diária do número de caminhões alugados por dia ( x ) é dada por:

Sabendo que o aluguel por dia é da ordem de U S $   300 e que a despesa total diária com a manutenção de cada veículo é igual a U S $   140 quando este é alugado e de U S $   15 , quando tal fato não ocorre, encontre:

  1. O número médio diário de caminhões alugados e o desvio padrão.
  2. A média e o desvio padrão do lucro diário

Passo 1

(a)

Se a gente chamar de X a v.a. que representa o número de caminhões alugados por dia. A gente já tem a tabela com os valores possíveis para X (0,1,2,3,4) e suas respectivas probabilidades.

Pra calcular o número médio de caminhões alugados é só calcular:

E X =   ∑ i = 1 n x i . p ( x i )

E X = 0 × 0,1 + 1 × 0,2 + 2 × 0,3 + 3 × 0,3 + 4 × 0,1

E X = 2,1

Passo 2

Pra calcular a variância usamos a fórmula:

s ² x = ∑ i = 1 n x i 2 . p x i - E X 2

s ² x = 0 2 × 0,1 + 1 2 × 0,2 + 2 2 × 0,3 + 3 2 × 0,3 + 4 2 × 0,1 - 2,1 2

s ² x = 1,29

Aí agora podemos calcular o desvio padrão que é a raiz quadrada da variância:

s x = 1,29 ≅ 1,14

Passo 3

(b)

Bom, nós sabemos que a definição de lucro é:

L u c r o = F a t u r a m e n t o - D e s p e s a s   t o t a i s

Nosso faturamento vai ser o aluguel das caminhonetes. Como o aluguel de cada uma custa U S $   300 :

F a t u r a m e n t o = 300 X

Onde X continua representando o número de caminhonetes alugadas por dia.

E nossas despesas totais? O enunciado diz que cada caminhonete alugada traz U S $   140 de despesas, ou seja:

D e s p e s a   d a s   a l u g a d a s = 140 X

E quando uma caminhonete não é alugada, a despesa que ela traz é de U S $   15 . Mas quantas caminhonetes não vão ser alugadas? O total de caminhonetes menos a quantidade que for alugada, certo? Ou seja, ( 4 - X ). Então temos que:

D e s p e s a   d a s   n ã o   a l u g a d a s = 15 ( 4 - X )

E as despesas totais serão a soma dessas duas aí:

D e s p e s a s   t o t a i s = 140 X + 15 ( 4 - X )

Passo 4

Nossa equação do lucro, substituindo tudo que achamos, fica assim então:

L u c r o = 300 X - 140 X + 15 4 - X = 160 X + 15 X - 60

L u c r o = 175 X - 60

Show! Agora podemos calcular o que foi pedido. Para a média do lucro, podemos “aplicar” a esperança dos dois lados da equação:

E L u c r o = E ( 175 X - 60 )

Fazendo a distribuiva...

E L u c r o = E 175 X - E ( 60 )

A constante que está multiplicando o X pode sair dos parênteses multiplicando a esperança, e a esperança de uma constante vale a própria constante, então...

E L u c r o = E 175 X - E 60 = 175 E X - 60

Mas já vimos na letra a) que E X = 2,1 , substituindo:

E L u c r o = 175 × 2,1 - 60 = 307,5

Essa aí então é a média do nosso lucro diário.

Passo 5

Para o desvio padrão, vamos seguir o mesmo raciocínio. Tirando a variância dos dois lados da equação do lucro:

L u c r o = 175 X - 60

V a r L u c r o = V a r ( 175 X - 60 )

Distributiva...

V a r L u c r o = V a r 175 X - V a r ( 60 )

A constante multiplicando o X sai da variância ao quadrado, e a variância de uma constante é igual a zero, então...

V a r L u c r o = V a r 175 X - V a r 60 = 175 2 V a r X - 0

V a r L u c r o = 175 ² V a r ( X )

Mas lá na letra a) vimos que a variância de X é 1,29 . Substituindo:

V a r L u c r o = 175 ² × 1,29 = 39506,25

Mas nós queremos o desvio padrão do lucro diário, então tira a raiz disso aí:

D P L u c r o = 39506,25 ≅ 198,76

Resposta

a   E X = 2,1   c a m i n h õ e s     ,     D P ( X ) ≅ 1,14   c a m i n h õ e s

b   E L u c r o = 307,5     ,     D P ( L u c r o ) ≅ 198,76

Exercício Resolvido #4

FONTE

Prove as expressões abaixo:

E a X + b = a E X + b

V a r a X + b = a 2 V a r X

Passo 1

1ª coisa: NÃO PIRA! Vamos com calma ok?

Vamos lembrar o que cada coisa é, ou seja, o que é média e variância ok?

E X = ∑ x . p x

Então jogando nessa fórmula teremos:

E a X + b = ∑ a X + b p ( a X + b )

Mas você concorda que:

P a X + b = P ( X )

Ou não?

Se não concorda, pensa comigo aqui rapidinho... Imagina um dado ok? Temos alguns possíveis resultados de X certo? Eles são...

X = 1,2 , 3,4 , 5,6

E temos que

P X = 1 = P X = 2 = … = P X = 6 = 1 6

Sim?

Agora imagina que usamos esse dado em um jogo de tabuleiro, onde temos uma regra que diz:

“O número de casas que o jogador deve avançar é o dobro do número obtido ao jogar os dados mais três casas.”

Opa! E aí? O que ele quis dizer?

N º   c a s a s   a v a n ç a d a s = 2 x + 3  

Entãão se jogarmos o dado e tiramos:

Nº do dado(X)

Nº de casas(Y)

1

2.1+3

5

2

2.2+3

7

3

2.3+3

9

4

2.4+3

11

5

2.5+3

13

6

2.6+3

15

Então temos novamente seis possibilidades? Podemos andar 5,7,9,11,13 ou 15 casas certo? Então percebe que podemos dizer que a probabilidade de:

P Y = 5 = P X = 1 = 1 6

E podemos dizer isso para todos? ((:

Então vamos continuar naquela expressão... Onde estávamos mesmo?

E a X + b = ∑ a X + b p a X + b = ∑ a X + b p X

E a X + b = ∑ a X . p x + b . p X = ∑ a X . p ( X ) + ∑ b p X = a ∑ X . p X + b ∑ p X

Epa! Olha só:

Então

E a X + b = a E X + b

Passo 2

Vamos olhar a outra expressão agora? Mas primeiro vamos relembrar a expressão de variância

V a r X = E X 2 - E X 2

Substituindo teremos

V a r a X + b = E a X + b 2 - E a X + b 2                                 ( i )

Desenvolvendo (produto notável!!!) & substituindo E a X + b = a E X + b ...

V a r a X + b = E a X 2 + 2 a b X + b 2 - { a E X 2 + 2 a b E X + b ² }                         ( i i )

Olhando para E a x 2 - 2 a b x + b 2 simbora desenvolver? Vamos usar a mesma lógica da primeira expressão que deduzimos (:

E a X 2 + 2 a b X + b 2 = E a 2 X 2 + 2 a b X + b 2 = a 2 E X 2 + 2 a b E X + b 2                       ( i i i )

Substituindo (iii) em (ii)

V a r a X + b = a 2 E X 2 + 2 a b E X + b 2 - a 2 E X 2 - 2 a b E X - b 2

Cancelando

V a r a X + b = a 2 E X 2 - a 2 E X 2 = a 2 E X 2 - E X 2

V a r a X + b = a 2 V a r ( X )

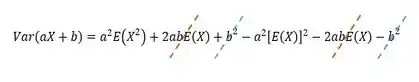
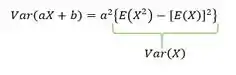
Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

UERJ-lista 1 prof Fabiano-20

Uma máquina do tipo caça-níqueis é composta por três discos que giram de forma independente, cada qual contendo as seguintes figuras: 2 laranjas, 3 bananas, 4 maçãs e 5 morangos. O apostador deve pagar 50 reais para jogar. Se sair 3 laranjas, ele ganha 250 reais; se sair 3 bananas, ganha 200 reais; se sair 3 maçãs, ganha 150 reais e se sair 3 morangos, ganha 100 reais; em qualquer outra situação ele perde. Pergunta-se: qual o lucro esperado de um jogador em uma jogada? E se o jogador fizer dez jogadas?

Passo 1

Tá, primeiro a gente tem que avaliar quais são as possibilidades de lucro que a gente tem.

E depois a gente calcula a probabilidade de cada uma acontecer, pra gente conhecer o lucro esperado.

Passo 2

Quais são os possíveis lucros ?

A gente sabe que independente do que sair, ele paga 50 reais.

Bom, quando sair 3 laranjas, ele recebe 250 reais, tendo um lucro de 200 reais. Concorda?

Pensando da mesma forma:

3   l a r a n j a s -   r e c e b e   250 - l u c r a   200

3   b a n a n a s - r e c e b e   200 - l u c r a   150

3   m a ç ã s - r e c e b e   150 - l u c r a   100

3   m o r a n g o s - r e c e b e   100 - l u c r a   50

Qualquer outro resultado que saia ele tem um prejuízo de 50 reais. Beleza?

q u a l q u e r   o u t r o   r e s u l t a d o - p r e j u í z o   d e   50

Passo 3

Organizando numa tabela pra ficar mais fácil:

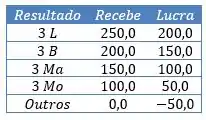
Agora vamos calcular a probabilidade de cada um desses lucros.

Passo 4

Pra calcular a probabilidade do cara lucrar 200 reais, é só a gente calcular a probabilidade de saírem 3 laranjas.

Em cada disco a gente tem um total de 14 possibilidades (14 imagens), sendo 2 delas laranjas. Então a probabilidade de sair uma laranja em um dos discos é:

P L = 2 14

Mas a gente quer P ( L ∩ L ∩ L ) , 3 laranjas nos 3 discos, que será:

P L ∩ L ∩ L = 2 14 × 2 14 × 2 14 = 8 2744

Passo 5

Pra calcular a probabilidade do cara lucrar 150 reais, é só a gente calcular a probabilidade de saírem 3 Bananas.

Em cada disco a gente tem um total de 14 possibilidades (14 imagens), sendo 3 delas bananas. Então a probabilidade de sair uma banana em um dos discos é:

P B = 3 14

Mas a gente quer P ( B ∩ B ∩ B ) , 3 laranjas nos 3 discos, que será:

P B ∩ B ∩ B = 3 14 × 3 14 × 3 14 = 27 2744

Passo 6

Fazendo o mesmo racicínio para as maçãs e os morangos a gente tem que:

A probabilidade de se lucrar 100 reais, que é a probabilidade de sair 3 maçãs é:

P M a ∩ M a ∩ M a = 4 14 × 4 14 × 4 14 = 64 2744

E a probabilidade de lucrar 50 reais será:

P M o ∩ M o ∩ M o = 5 14 × 5 14 × 5 14 = 125 2744

Passo 7

Falta só calcular a probabilidade de qualquer outro resultado sair, fazendo o cara ter prejuízo de 50 reais.

Pensa comigo!

P q u a l q u e r   o u t r o   r e s u l t a d o = 1 - ∑ P d o s   r e s u l t a d o s   q u e   a   g e n t e   j á   c a l c u l o u

Concorda ?

∑ P d o s   r e s u l t a d o s   q u e   a   g e n t e   j á   c a l c u l o u = 8 2744 + 27 2744 + 64 2744 + 125 2744 = 224 2744

Logo:

P q u a l q u e r   o u t r o   r e s u l t a d o = 1 - 224 2744

= 2520 2744

Passo 8

Vou montar uma tabelinha agora com os possíveis lucros que o jogador pode ter e a probabilidade de cada um acontecer, tranquilo?

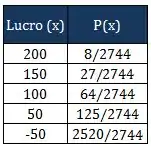
Passo 9

Chamando de X a v.a. que representa o lucro de um jogador em uma jogada.

Pra gente saber o lucro médio pra uma jogada, a gente tem que calcular a esperança dessa variável.

Como se trata de uma variável discreta (que assume valores específicos: 200, 150, 100, 50 e -50), a esperança é dada por:

E X =   ∑ i = 1 n x i . p ( x i )

Usando a nossa tabela...

E X = 200 × 8 2744 + 150 × 27 2744 + 100 × 64 2744 + 50 × 125 2744 - 50 × 2520 2744

E X ≅ - 39,25

Passo 10

Agora pra saber o lucro esperado de 10 jogadas, a gente precisa calcular:

E 10 . X =   ?

Concorda ?

Usando as propriedades da esperança a gente tem que:

E 10 . X = 10 × E X

Que a gente já calculou.

E 10 . X = 10 × - 39,25

E 10 . X ≅ - 392,5

Resposta

E X ≅ - 39,25           e         E 10 . X ≅ - 392,5

Exercício Resolvido #6

UNESP – Profs Alexandre Lima e Moraes Junior

Um empresário, investindo em um determinado empreendimento, espera ter os seguintes lucros em função dos cenários “Bom”, “Médio” e “Ruim”:

A esperança e a variância do lucro são, em R$ e R $ 2 , respectivamente,

  1. 5.500,00 e 3.160,00
  2. 5.300,00 e 3.510,00
  3. 5.300,00 e 3.160,00
  4. 5.000,00 e 3.510,00
  5. 5.000,00 e 3.160,00

Passo 1

A esperança conseguimos achar fazendo a continha:

E X = 8 × 0,25 + 5 × 0,60 + 2 × 0,15  

Então temos que o valor da esperança é

E X = 5,3   m i l = 5.300,00

Passo 2

Para encontrar a variância, vamos calcular antes E ( X 2 )

E X 2 = 8 2 × 0,25 + 5 2 × 0,60 + 2 2 × 0,15  

Assim,

E X 2 = 31,6   m i l  

Passo 3

Agora sim, calculando a variância:

V a r X = 31,6 - 5,3 2 = 3.510,00

Resposta

Letra (B).

Exercício Resolvido #7

IFES – Engenharia de Minas – Lista de Probabilidade de Estatística

Um empresário comercializa mármore para o exterior. Esse material de produção do mármore pode estar defeituoso com probabilidade de 0,02 e, nesse caso, ela tem probabilidade 0,5 de ser recuperável. O custo de cada placa produzida é 1.200 u.m, que será acrescido de mais 50,00 u.m se precisa ser recuperada. As irrecuperáveis são descartadas. Sabendo que cada peça é vendida a 3.500 u.m, encontre a distribuição da variável aleatória “lucro por peça produzida”.

  1. Qual é o Lucro médio por peça produzida?
  2. Em uma produção de 10.000 peças, qual é o lucro esperado?

Passo 1

Antes de resolvermos as letras (a) e (b) vamos nos organizar.

Vamos considerar a variável L: Lucro. Logo,

Podemos representar esse resultado acima através da árvore de probabilidade. Porém antes considere a seguinte notação:

A: com defeito

S: sem defeito

R: recuperável

D: descartada

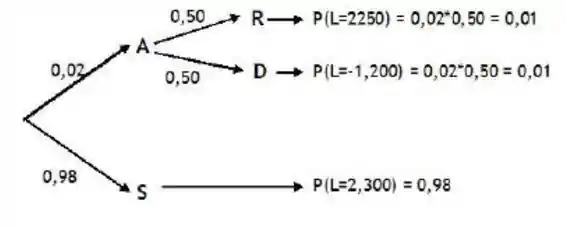
Assim, a distribuição da variável aleatória lucro é dada por:

Passo 2

  1. Agora vamos usar as informações acima para calcular o lucro médio.

    2. E L = - 1200 × 0,01 + 2250 × 0,01 + 2300 × 0,98

    Fazendo as continhas, concluímos que o Lucro médio por placa produzida é de R $   2264,50

    E L = 2264,50

    Passo 3

  2. Em uma produção de 10.000 peças o lucro esperado pode ser calculado da seguinte forma

10000 × E L = 2264,50

Portanto,

E L = 22.645.000

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

IFES – Engenharia de Minas – Lista de Probabilidade de Estatística

Um empresário faz um estoque de um produto que custa R $ 0,50 e que ele vende a R $ 1,50 no primeiro dia em que o produto está na loja. Todo produto que não é vendido nesse primeiro dia não serve mais e é jogado fora. Seja X a variável aleatória que denota o número de produtos que os fregueses compram em um dia casualmente escolhido. O empresário descobriu que a função de probabilidade X é dada por

Quantos produtos deveria o empresário ter em estoque a fim de maximizar a média (valor esperado) do lucro?

Passo 1

Vamos entender qual valor esperado teremos para as quantidades de produto em estoque:

  • Para 1 produto no estoque, temos que o valor esperado do lucro será:

    • E L =   - 0,50 × 0,1 + 1 × 0,9 → E L = 0,85

  • Para 2 produtos no estoque, temos que o valor esperado do lucro será:

    • E L =   - 1,00 × 0,1 + 0,50 × 0,4 + 2 × 0 , 3 → E L = 0,7

  • Para 3 produtos no estoque, temos que o valor esperado do lucro será:

E L =   - 1,50 × 0,1 + 0,00 × 0,4 + 1,50 × 0,3 + 3,00 × 0,2 → E L = 0,90

Portanto, conseguimos concluir que 2 produtos no estoque é capaz de maximizar o lucro do proprietário.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #9

IFES – Engenharia de Minas – Lista de Probabilidade de Estatística

O tempo T , em minutos, necessário para um operário processar certa peça é uma variável aleatória com a seguinte distribuição de probabilidade:

  1. Calcule o tempo médio de processamento.
  2. Para cada peça processada, o operário ganha um fixo de R $ 2,00 mas, se ele processa a peça em menos de seis minutos, ganha R $ 0,50 em cada minuto poupado. Por exemplo, se ele processa a peça em quatro minutos, ganha a quantia adicional de R $ 1,00 . Encontre a distribuição, a média e a variância da variável aleatória.

Passo 1

  1. O tempo médio de processamento pode ser calculado como

    2. E L = 2 × 0,1 + … + 7 × 0,1 = 4,60

  2. A distribuição da v.a lucro será

E L =   4 × 0,1 + … + 2 × 0,3 = 2,75

Assim,

E L 2 =   4 2 × 0,1 + … + 2 2 × 0,3 = 7,975

Então, a variância será

V a r S = 7,975 - 2,75 2 = 0,4125

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #10

Notas de Aula – Jair Donadelli

Seja X o número de carros lavados num lava-rápido em 1 hora.

Calcule E ( 2 X - 1 ) .

Passo 1

Nesse exercício nós vamos utilizar as propriedades da Esperança que muitas das vezes não damos valor mas podem nos ajudar em alguns casos (e muito!) rs.

Sabemos que E 2 X - 1 = 2 E X - 1 pelas propriedades.

Então,

2 E X - 1 = 2   ∑ x x f x - 1 = 2   41 6 - 1 = 12,67

Show de bola?!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Seja X o dano (em valor monetário) incorrido por um determinado tipo de acidente em um ano. Os valores possíveis de X são 0, 1000, 5000 e 10000, com probabilidades 0,8, 0,1, 0,08 e 0,02 respectivament
Uma empresa de fornecimento de materiais químicos atualmente possui em seu estoque 100 libras de um determinado produto, vendido aos clientes em lotes de 5 libras. Seja X = número de lotes pedidos por
Um indivíduo que possui um seguro de automóvel de uma determinada empresa é selecionado aleatoriamente. Seja Y o número de infrações ao código de trânsito para as quais o indivíduo foi reincidente nos
Suponha que o número de certo tipo de planta encontrada em uma região retangular (denominada quadrat pelos ecologistas) em uma determinada área geográfica seja uma va X com fmp
Seja X resultado de um dado lançado uma vez. Se antes de lançar o dado, oferecessem a você (1/3,5) dólares ou h(X) 1/X dólares, você aceitaria a quantia garantida ou faria a aposta? [Nota: Normalmente