Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e estão mostrados abaixo respectivamente.
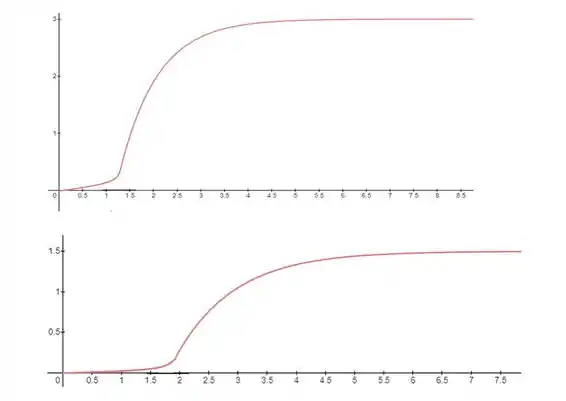
Sintonize ambos os controladores da malha cascata utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária. Suponha um controlador PI secundário e um PID primário
Passo 1
A sintonia do controle em cascata sempre é feita de dentro para fora, sendo assim, o primerio passo sempre será controlar o controlador mais interno, ou seja, o controlador secundário. Sendo assim, vamos definir a função FOPDT para a malha interna:
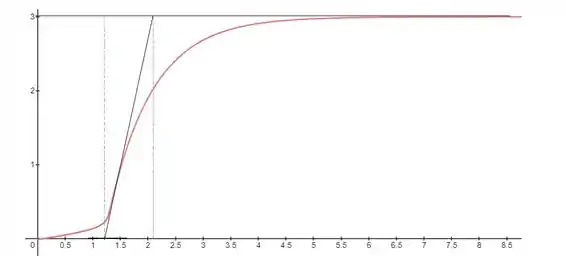
Dessa forma, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador PI:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Para sintonizar o segundo controlador, precisamos determinar a função FOPDT para a variável primária:
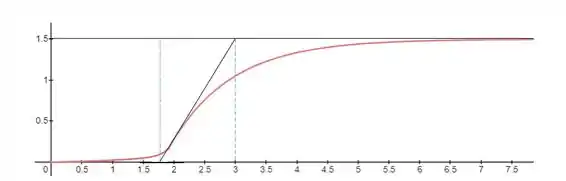
Com esse esboço, podemos estimar nossas constantes como:
Com esses valores, conseguimos sintonizar o PID usando a tabela abaixo:

Como o controlador secundário foi um PI e o primário será um PID, as correlações que usaremos serão as do último quadrante da tabela acima.
Entretanto, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Sendo assim, estamos dentro das especificações.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
Portanto, teremos o seguinte controlador PID primário: