Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:
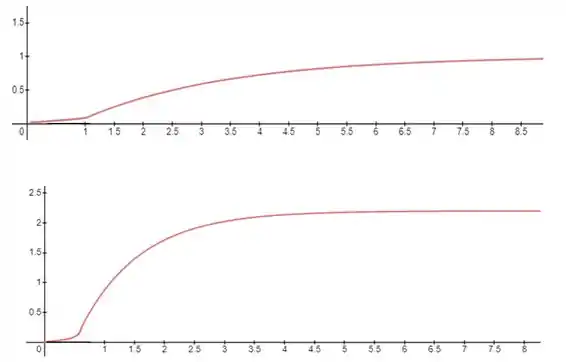
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo P e o primário é do tipo PI.
Passo 1
Como a sintonia em cascata sempre é feita de dentro para fora, primeiro devemos sintonizar a malha secundária. Para isso, vamos tentar descobri os parâmetros FOPDT a partir do gráfico dado:
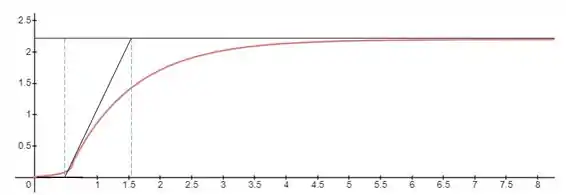
Dessa forma, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador P:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Agora que já sintonizamos o controlador secundário, podemos partir para o primário. Sendo assim, vamos fazer o mesmo que fizemos anteriormente para a variável primária:
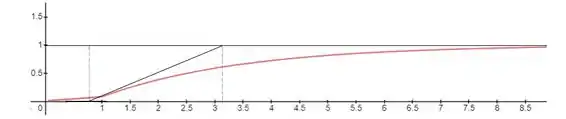
Com esse esboço, podemos estimar nossas constantes como:
Agora, vamos consultar a tabela com as correlações de Austin e Loez para saber quais correlações deverão ser usadas.

O nosso controlador secundário era do tipo P, e o primário será do tipo PI, logo, devemos usar as correlações que estão no canto superior esquerdo da tabela.
Porém, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Maravilha! Tudo certo.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
O nosso PI primário ficará portanto