Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:
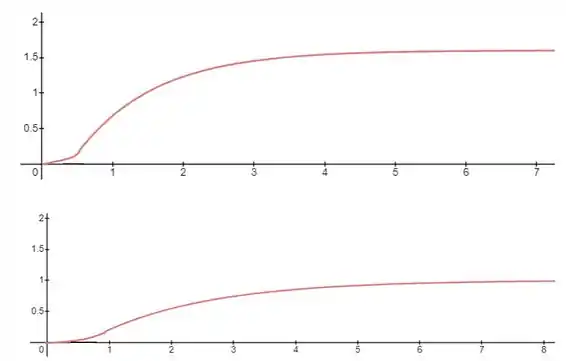
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo PI e o primário é do tipo PID.
Passo 1
Devemos sempre começar pelo controlador mais a dentro na malha, nesse caso, o controlador secundário. Vamos primeiro estimar os parâmetros da FOPDT dessa malha usando o esboço abaixo:
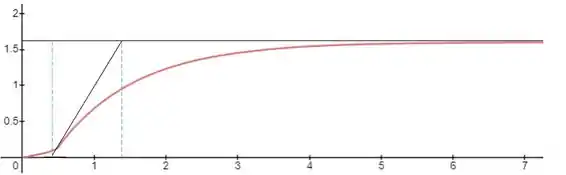
Com esse esboço, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador PI:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Vamos aplicar o mesmo procedimento agora para estimar a função FOPDT para a malha primária:
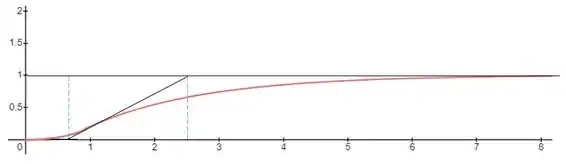
Com esse esboço, podemos estimar nossas constantes como:
Agora, podemos sintonizar o controlador primário consultando a tabela abaixo:

Nesse exercício o controlador secundário é PI e o primário é PID, então usamos as correlaçãoes que estão no canto inferior direito da tabela.
Porém, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Maravilha! Tudo certo.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
O nosso PI primário ficará portanto