Dualidade Onda-Partícula e Princípio da Incerteza
Produzido por Marcelo BrillantinoTeoria
Dualidade Onda-Partícula: dupla-fenda de Young
A gente viu que o efeito fotoelétrico trouxe evidências de que a luz é constituída por partículas: os fótons.
Mas, se a luz é constituída por partículas, como é que a gente explica o seu comportamento ondular?
Tipo assim, fizemos vários exercícios de comprimento de onda, radiação, etc. E todas essas são características ondulares.
Além disso, uma das maiores provas da natureza ondular da luz são os fenômenos de difração que podem ser vistos no experimento de dupla-fenda de Young.
Se a luz tivesse comportamento puramente particular, ao passar luz por duas fendas em uma parede, o resultado observado seria mais ou menos esse:
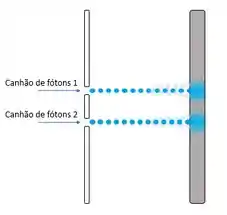
Mas o que realmente é observado é mais parecido com isso:
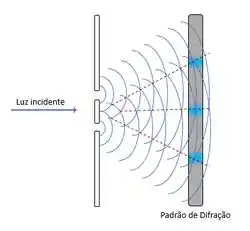
Ao invés de duas marcas no “detector”, o padrão de interferência mostra diversas marcas.
Toda vez que duas ondas se cruzam em pontos de máximo, elas sofrem interferência construtiva e suas amplitudes aumentam, sendo detectado no nosso padrão de difração como um ponto azul.
Se duas ondas se encontram fora de fase, com o máximo de uma fora do máximo da outra, a interferência é destrutiva e a amplitude diminui (podendo até zerar) tanto que a onda não é detectada no nosso padrão de difração (ausência de ponto azul).
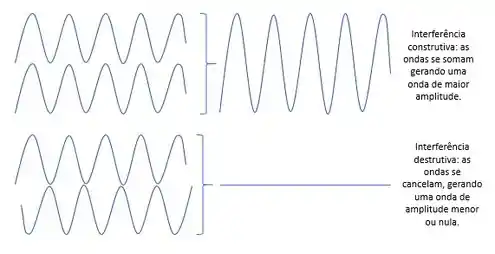
Então o efeito fotoelétrico prova que a luz é partícula, enquanto os padrões de interferência provam que a luz é onda.
E AGORA??? O que é a luz?
A LUZ É OS DOIS!!! Ela tem características ondulares e características corpusculares (particulares).
Ainda não conseguimos juntar as duas coisas na mesma teoria. Então usamos cada uma delas de acordo com a situação.
Ou seja: quando for melhor pra gente pensar na luz como onda, usar , etc.. fazemos isso; quando for mais conveniente pensar em fótons, energia do fóton, efeito fotoelétrico, etc... aceitamos o comportamente particular e vamossimbora.
De Broglie e a dualidade do elétron
Mas se a radiação, que antes era onda, agora é partícula e onda ao mesmo tempo, por que que o elétron, que até então era partícula, não pode ser partícula e onda ao mesmo tempo?
A história é confusa mesmo. Acontece que o elétron também faz algumas coisas que só são explicadas se considerarmos ele como partícula, mas faz outras que fazem mais sentido se pensarmos nele como onda.
Por isso dizemos que ele tem natureza ou comportamento dual onda-partícula, assim como a luz.
Quem disse isso primeiro foi De Broglie. Ele juntou algumas fórmulas de Einstein e Planck em uma só:
Onde é o nosso tão querido comprimento de onda, é a constante de Planck (6,626.10-34 J.s) e (às vezes chamado de ) é o momento linear (às vezes chamado de quantidade de movimento).
Como , a forma mais usada da equação de De Broglie é assim:
E olha que doido!!! Na mesma equação a gente tá usando , que é puramente ondular, e (massa), que é puramente particular.
Segundo De Broglie, então, não só o elétron tem característica dual, mas todas as partículas.
Toda vez que a gente coloca a massa e a velocidade da partícula na fórmula ali de cima, existe um comprimento de onda associado.
No mundo macroscópico, isso tem pouca interferência porque a dimensão do comprimento de onda em relação à dos corpos é muuuuuito pequena e pode ser completamente ignorada.
Mas no mundo dos elétrons, prótons, nêutrons.. isso faz muita diferença. Na quântica, a fronteira entre onda e partícula é muito tênue. É como se o elétron fosse às vezes onda, às vezes partícula. Ou, se você for capaz de aceitar: ele é as duas coisas ao mesmo tempo.
Princípio da Incerteza
Dá uma olhada na figura aí de baixo:
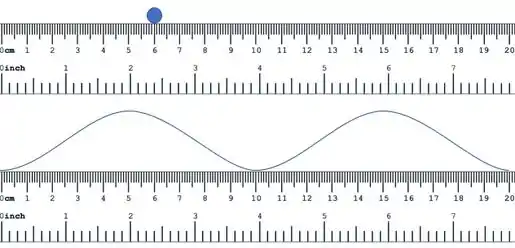
A gente pode ver que a bolinha está na posição de 6 cm. Mas qual a posição da onda?
Difícil né?!
Até podemos dizer que a onda está sobre a régua e tem seus máximos nas posições 5 e 15 cm. Mas a onda está em toda a reta, e não em uma posição especifica!
Lá no começo da nossa conversa sobre átomos, a gente comentou que o conceito de trajetória não faz muito sentido na quântica. Esse é um conceito clássico.
Quando a gente começa a considerar a característica dual do elétron, pela equação de De Broglie, se a gente especifica a massa e a velocidade do elétron, então sabemos que existe um comprimento de onda associado. E não podemos localizar uma onda.
O que que isso significa?
Significa que se você sabe exatamente a massa e a velocidade do elétron, você não tem como determinar a posição dele.
Agora, por outro lado, se você sabe a massa e a posição exatas, então não podemos calcular a velocidade. Não sabemos para onde ele está indo.
Essa relação entre momento linear () e posição () é chamada de complementaridade. Quanto mais certeza a gente tem do valor do momento , menor certeza se tem do valor da posição .
Então a incerteza da posição e a incerteza do momento são inversamente proporcionais.
Pelo Princípio da Incerteza de Heisenberg:
Onde é a incerteza do momento, é a incerteza da posição e o , chamado de “h cortado” ou “h barrado” equivale à constante de Planck dividida por .
Esse é considerado um valor “mínimo”. Isso porque a gente pode não saber nada da posição e nada do momento, e aí ambas as incertezas vão para o infinito. A relação de Heisenberg é uma situação limite que diz que, uma vez que uma das incertezas seja conhecida, a outra tem que ser maior ou igual a determinado valor, calculado pela relação.
Muitas vezes consideramos que as massas são conhecidas com incertezas irrelevantes. Então toda a incerteza do momento se deve, na verdade, à incerteza na velocidade. Nesse caso o princípio de Heisenberg fica assim:
Importante: Caso a incerteza da posição seja dada com o sinal de na frente, a gente considera o como duas vezes o valor indicado.
Ou seja, para uma incerteza na posição de :
A final de contas o é toda a amplitude do intervalo que a posição pode ocupar.
O mesmo vale para a velocidade!
Resumindo...
- Vimos que a luz tem características de onda e características de partícula;
- Vimos que o elétron tem características de onda e características de partícula;
- Vimos que, como o elétron tem natureza ondulatória, não podemos especificar sua posição, caso a gente já saiba a velocidade e a massa do mesmo;
E para os fãs de Breaking Bad: o nome do princípio da incerteza não parece estranho né?

Falow, valew. Bora calcular!
De Broglie e a dualidade do elétron
Princípio da Incerteza
Resumindo...
Exercícios Resolvidos
Exercício Resolvido #1
UFG – Lista de Exercícios de Química Geral. Professora Helen. Questão 25.
O que significa dualidade onda-partícula?
Passo 1
A dualidade onda partícula é uma propriedade que permite que algumas coisas se comportem tanto como onda quanto como partícula.
Isso significa que as ondas podem se comportar como partículas e as partículas podem se comportar como ondas.
É o caso da luz, que possui comprimento de onda e frequência (características de onda), mas por vezes se comporta como partícula (fótons), como no efeito fotoelétrico.
Segundo De Broglie, todos os corpos possuem características ondulatórias e características particulares. Acontece que, no mundo macro, as características de onda são muito pequenas em relação as características de partícula, podendo ser desprezadas.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.1.
Quando J.J. Thomson fez seus experimentos em raios catódicos, a natureza do elétron estava em dúvida. Alguns o imaginavam como uma forma de radiação, como a luz; outros acreditavam que o elétron era uma partícula. Algumas das observações feitas com raios catódicos eram usadas para apoiar outra visão. Explique como cada uma das propriedades seguintes dos raios catódicos pode apoiar o modelo de partícula ou de onda do elétron.
- Eles passam através de folha de metal.
- Eles viajam em velocidades inferiores à da luz.
- Se um objeto é colocado em sua trajetória observa-se uma sombra.
- Sua trajetória muda quando eles passam entre placas com carga elétrica.
Passo 1
Pois é, hoje a gente sabe que os elétrons tem características de onda e características de partícula. Mas no tempo de Thomson, ainda estavam tentando dizer se ele era uma coisa OU outra. E a gente vai analisar cada uma das propriedades expostas no enunciado pra ver que a confusão tem motivo mesmo: alguns resultados apontam pra partícula e outros pra onda.
Passo 2
a) Eles passam através de folhas de metal.
A explicação para uma partícula passar por uma placa de metal é: existe um buraco. Se a placa não tem nenhum furo por onde o elétron passar, ele só passa se tiver características ondulares. Então, essa primeira afirmativa indica que o elétron é onda.
Passo 3
b) Eles viajam em velocidades inferiores à da luz.
Essa afirmativa indica o comportamento particular do elétron. Se o elétron fosse puramente uma radiação eletromagnética, ele deveria ter a mesma velocidade ds demais ondas eletromagnéticas: a velocidade da luz. Como os elétrons são partículas carregadas, existem forças de repulsão agindo entre eles, o que “atrasa” os movimentos, diminuindo a velocidade para algum valor menor que a velocidade da luz.
Passo 4
c) Se um objeto é colocado em sua trajetória observa-se uma sombra.
Essa alternativa é complicada, mas ela apoia que o elétron é uma partícula.
Olha só: se uma partícula está viajando em linha reta e algo fica na frente dela, ela não consegue passar. Caso a gente tenha colocado um detector no final da trajetória, a gente não vai detectar a partícula, só uma sombra.
Já a radiação, pelo fenômeno da difração, consegue “driblar obstáculos”, e a sombra não é observada.
Passo 5
d) Sua trajetória muda quando eles passam entre placas com carga elétrica.
Essa coisa de mudar de trajetória por causa de campo elétrico (placas com carga elétrica) é coisa de partícula carregada né?
Então a última alternativa apoia a hipótese de que o elétron é partícula. E carregada.
Resposta
- Onda
- Partícula
- Partícula
- Partícula
Exercício Resolvido #3
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex. 1.8.
Explique por que não podemos observar o comportamento ondulatório de um objeto macroscópico como uma bola de ping-pong?
Passo 1
É, segundo De Broglie, todos os corpos apresentam comportamento ondulatório.
Então por que que a gente não consegue “ver esse comportamento” no nosso dia-a-dia?
Por que no mundo macroscópico as características ondulatórias são muito pequenas em relação as corpusculares. São irrelevantes mesmo.
Passo 2
Vamos usar como exemplo a bolinha de ping-pong do enunciado.
Vamos supor que ela tenha 5 cm de diâmetro e pese 10 g (0,01 kg). A bolinha é jogada a 30 m/s. Qual seria o comprimento de onda dessa bolinha?
Tá vendo aquele valor de comprimento de onda? Cara, aquilo ali é 0,00000000000000000000000000000000221 metros. É tipo nada. É impossível de observar. É da dimensão do elétron.
Por isso que as características ondulatórias são geralmente ignoradas no estudo de objetos macro :)
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 14-exemplo 1.6.
Para apreciar o porquê de as propriedades de onda das partículas não serem facilmente detectadas, calcule o comprimento de onda de uma partícula de massa 1g viajando em 1m.s-1.
Passo 1
Vamos aplicar De Broglie, sabendo que e .
Obs: 1 J = 1 kg.m²/s²
Passo 2
O que a gente conclui com isso?
Que o comprimento de onda é muito pequeno para ser “percebido”. Essa observação é válida para qualquer objeto visível que viaje em velocidades normais.
Resposta
.
Exercício Resolvido #5
USP/IQSC– Lista de Exercícios de Química Geral – Estrutura Atômica. Questão 10.
Calcule o comprimento de onda de uma moto Harley Davidson cuja massa é de aproximadamente 330 kg (moto + piloto) viajando a 230 km/h.
Passo 1
Tá pedindo o comprimento de onda de um objeto.. De Broglie!!!
Sabendo que:
Obs: pra passar a velocidade pra metro por segundo, pode só multiplica por 0,28 também tá?!
Passo 2
Por De Broglie:
Então o comprimento de onda associado à moto do enunciado é igual a 3,14.10-38 m.
Resposta
.
Exercício Resolvido #6
UFRJ – Lista de Exercícios de Química Geral I – Estequiometria, Teoria Atômica e Classificação Periódica. Professor Emerson. Questão 6.
Utilize a relação de De Broglie para determinar os comprimentos de onda dos seguintes objetos:
- Uma pessoa de 85 kg esquiando a 50 km/h;
- Uma bala de revólver de 10,0 g detonada a 250 m/s;
- Um átomo de lítio movimentando-se a 2,5.105 m/s.
Passo 1
O enunciado já tá falando que a gente precisa usar a relação de De Broglie. Então é só se ligar nas unidades e aplicar:
Lembrando que:
Passo 2
a) Uma pessoa de 85 kg esquiando a 50 km/h.
Então o comprimento de onda associado à pessoa do item “a” é igual a 5,61.10-37 m.
Passo 3
b) Uma bala de revólver de 10,0 g detonada a 250 m/s.
Então o comprimento de onda associado à bala de revólver do item “b” é igual a 2,65.10-34 m.
Passo 4
c) Um átomo de lítio movimentando-se a 2,5.105 m/s.
Ops! E a massa? Se não é dada, tem que olhar na tabela periódica!
Vamos ver.. O lítio tem 3 próton e 4 nêutrons. Portanto, massa atômica igual a 7 u.a.
Mas a gente precisa dessa massa em kg certo?
Então precisamos da conversão:
E joga tudo na relação de De Broglie:
Então o comprimento de onda associado ao átomo de lítio do item “c” é igual a 2,28.10-13 m.
Vale a pena destacar que somente no item “c” a dimensão do comprimento de onda em relação à dimensão do objeto estudado é significante.
Não só porque 10-13 m >>> 10-34 m, mas principalmente porque a dimensão do átomo é muito menor que a dimensão da pessoa esquiando ou mesmo da bala de revólver.
No mundo dos objetos visíveis de velocidades “normais” os comprimento de onda são tão pequenos em relação às dimensões dos corpos, que o comportamento ondulatório pode ser ignorado.
Resposta
a) .
b) .
c) .
Exercício Resolvido #7
UFRRJ – Lista de Exercícios de Química Geral – Estrutura Atômica. Questão 1.26.
Um átomo de um elemento desconhecido viaja com 15% da velocidade da luz. O comprimento de onda de De Broglie deste átomo é de 1,06.10-16 m. Identifique o elemento.
Passo 1
Pela relação de De Broglie.
A gente sabe que:
E o enunciado nos diz que:
Na relação de De Broglie, então, só tá faltando a massa. Que é justamente o que ele nos pede pra calcular.
Passo 2
Então a massa do átomo é de 1,39.10-25 kg.
Passo 3
Pra descobrir qual é o elemento, vamos ter que passar essa massa aí pra unidades atômicas.
E a relação pra conversão é a seguinte:
Então a massa do átomo em unidades atômicas é dada por:
Agora vamos ter que procurar na tabela periódica quem é o elemento cujos átomos tem massa de 83,7 u.a.
Com aproximadamente essa massa apareceu o criptônio: .
Elemento identificado!
Resposta
.
Criptônio.
Exercício Resolvido #8
UFRRJ – Lista de Exercícios de Química Geral – Estrutura Atômica. Questão 1.21.
Nêutrons térmicos são nêutrons se movendo a velocidades comparáveis à de partículas no ar em temperatura ambiente. Estes nêutrons são efetivos na inicialização de reações nucleares em cadeia entre isótopos do 255U. Calcule o comprimento de onda (em nm) associado com um feixe de nêutrons se movendo a 7,0.102 m/s. (Massa do nêutron = 1,67.10-27 kg).
Passo 1
Pela relação de De Broglie.
A gente sabe que:
E o enunciado nos diz que:
Na relação de De Broglie, então, só tá faltando o comprimento de onda. Que é justamente o que ele nos pede pra calcular.
Passo 2
Mas o enunciado pede em nanômetros:
Então o comprimento de onda do “nêutron térmico” do enunciado é igual a 0,567 nm.
Resposta
.
Exercício Resolvido #9
UFRRJ – Lista de Exercícios de Química Geral – Estrutura Atômica. Questão 1.23.
Suponha que fótons de luz vermelha (675 nm) sejam usados para localizar a posição de uma bola de ping-pong de massa 2,8 g em movimento onde a incerteza na posição da bola é igual a um comprimento de onda. Qual a incerteza mínima na velocidade da bola de ping-pong? Comente a magnitude deste resultado.
Passo 1
Pelo Princípio de Heisenberg:
Precisamos calcular a incerteza da velocidade () e sabemos que:
Tudo nas suas devidas unidades. Então é só jogar na fórmula e calcular o que nos interessa!
Passo 2
Calculando:
E a incerteza mínima da velocidade da bolinha de ping-pong é de 2,79.10-26 m.s-1.
Passo 3
Em relação à magnitude:
10-26 metros é muuuuito menor que a dimensão da bolinha (que fica na ordem de 10-3) e definitivamente imperceptível aos olhos humanos.
Assim, considerar essa incerteza em cálculos de velocidade da bolinha ou energia cinética ou o que quer que seja é completamente irrelevante.
Resposta