21 – O uso de fluidos supercríticos na fase móvel em SFC depende de suas propriedades como solventes não polares. O parâmetro de solubilidade, δ, é definido como
Onde, ΔUcoesão é a energia de coesão do solvente, ou seja, a energia necessária para aumentar isotermicamente o volume do solvente até um valor infinito. O dietil-éter, o tetracloreto de carbono e a dioxana apresentam faixas do parâmetro de solubilidade de 7-8, 8-9, e 10-11, respectivamente.
A) Obtenha uma equação prática para o cálculo das isotérmicas que mostram a variação da energia interna reduzida, ΔUr(Tr, Vr), definida por
B) Trace um gráfico de ΔUr contra pr para as isotermas Tr = 1; 1,2; e 1,5 na faixa de pressão reduzida para o qual 0,7 ≤ Vr ≤ 2.
C) Trace um gráfico de δ contra pr para as isotermas Tr = 1 e 1,5 do dióxido de carbono na faixa de pressão reduzida para o qual 1 ≤ Vr ≤ 3. Em que faixa de pressão, a Tr = 1, o dióxido de carbono terá propriedades de solvente semelhantes às do tetracloreto de carbono líquido?
(Sugestão. Use um programa matemático ou uma planilha eletrônica.)
Passo 1
A)
Podemos usar a eq. de estado de Dieterici para determinarmos uma relação para a pressão reduzida, pr.
A eq. de estado de Dieterici é suposto ter uma boa precisão em pontos próximos do ponto crítico. Ela é muito falha em altas densidades onde Vm começa a se aproximar do valor do coeficiente de Dieterici b. Nós vamos usar essa equação para derivar a equação prática para o cálculo das isotermas
Pela tabela 1.7:
Passo 2
Vamos derivar a equação de estado de Dieterici em relação a temperatura Tr, na condição de volume constante Vr
Assim,
Passo 3
Pela eq. 3.48:
Substituindo:
Assim,
Passo 4
Para acharmos a variação de energia interna reduzida ΔUr(Tr, Vr), basta nós aplicarmos integral em ambos os lados da equação que encontramos anteriormente:
Assim,
Como se trata da energia de coesão que é a energia necessária para aumentar isotermicamente o volume do solvente até um valor infinito, assim devemos integrar sob um intervalo de Vr a Tr constante até Vr igual a infinito, logo
Passo 5
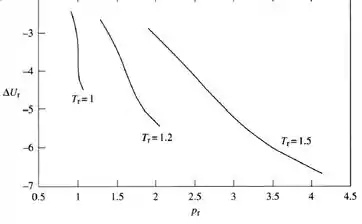
B)
Com a equação acima para a variação de energia interna, e com um software matemático, por exemplo, Matlab ou Python, vamos obter o seguinte gráfico:
Passo 6
C)
Temos a seguinte equação que relaciona matematicamente o parâmetro δ com a pressão reduzida pr:
Onde, para a pressão critica pc possui um valor de pc = 72,9 atm.
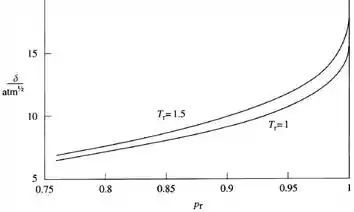
Analisando o gráfico acima podemos ver que a faixa de pressão, em Tr = 1, que o dióxido de carbono tem propriedades de solvente semelhantes às do tetracloreto de carbono líquido é nas faixas de valores de δ para:
Nessa faixa a pressão reduzida possui valores de:
Resposta
A)
B)
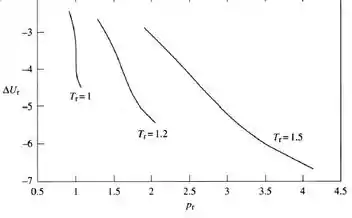
C)