Os seguintes dados foram obtidos para uma amostra de gás contendo de moléculas em um recipiente rígido. (a) Determine o volume da amostra. (b) Lance os dados em um gráfico, a mão ou com o auxílio de um computador. Agora, suponha que você adicionou mais de moléculas de gás mas manteve fixo o volume. Lance os dados da segunda amostra em um gráfico. (c) Em que temperatura (em Kelvins) as duas linhas se cruzam?

Passo 1
a) Queremos aqui encontrar o volume da amostra, para isso podemos usar e equação dos gases ideais explicitada para .
Aqui, é a pressão, é o volume, é o número de mol, é a contante dos gases ideias e é a temperatura. Os dados para o cálculo do volume são os seguintes:
Substituindo na equação acima temos:
Portanto o volume da amostra 1 é de aproximadamente , se calcularmos os volumes para as outras amostras com preção e temperatura distintas, iremos perceber que o volume é aproximadamente a . Uma tabela feita no computador mostra os volumes para as temperaturas e pressões dada na tabela acima:

Passo 2
b) Para os dados abaixo fornecidos no enunciado, com e kelvin e em temos a seguinte tabela:

Para a tabela acima temos o seguinte gráfico:
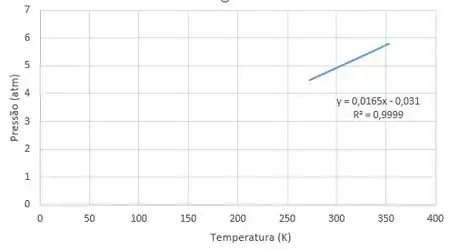
Agora queremos fazer um gráfico em que aumentos o número de mol de para , e mantemos o volume constante. Isso irá fazer a pressão do sistema aumentar. Logo precisamos calcular a pressão para cada temperatura dada.
Podemos calcular a nova pressão com a equação dos gases ideais explicitada para pressão.
Substituindo os seguintes valores nela teremos:
Calculando a pressão para as temperaturas indo de a , seguindo o mesmo passo acima, termos a seguinte tabela:
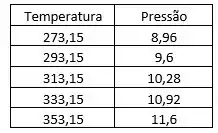
Para a tabela acima temos o seguinte gráfico:
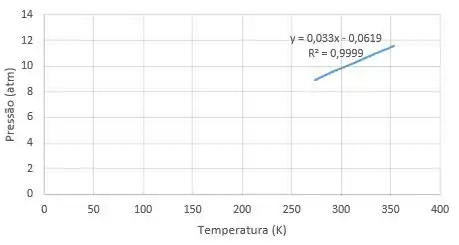
Passo 3
c) Em que temperatura (em Kelvins) as duas linhas se cruzam?
Para encontra a temperatura qual as duas linhas se cruzam, basta igual a equação das restas dos dois gráficos.
Pra o primeiro gráfico em que a equação da reta é a seguinte:
Pra o segundo gráfico em que a equação da reta é a seguinte:
Igualando as duas equações temos:
Resposta
a)
b) Para
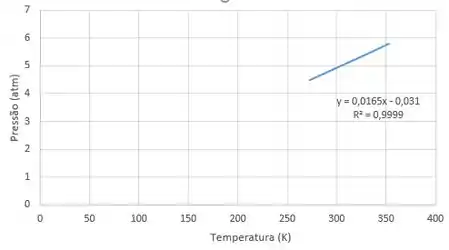
Para

c)