Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 10.Problemas Numéricos - Ex. 4
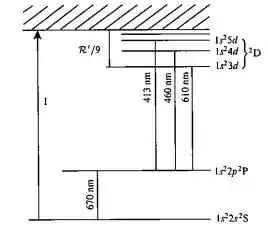
Uma série de linhas do espectro dos átomos de Li neutros provém das combinações de com e tem os comprimentos de onda 610,36 nm, 460,29 nm e 413,23 nm. Os orbitais d são hidrogenóides. Sabe-se que o termo está 670,78 nm acima do estado fundamental, que é . Calcule a energia de ionização do estado fundamental do átomo. Dica: O gráfico abaixo pode o ajudar.
Passo 1
E aí, genteee! Tudo bem? Vamos olhar o gráfico dado pra gente!
O menor valor possível de n em 1s²nd¹ é 3, portanto as séries de termos D² corresponde a 1s²3d, 1s²4d, etc. A figura acima aí mostra uma descrição consistente com os dados do problema. Se assumirmos que as energias dos orbitais d são hidrogênicos, nós podemos escrever a seguinte equação ó:
Para as transições , nós temos que:
Passo 2
A partir da equação acima, olha o que a gente poderia escrever então:
Note que o enunciado nos deu os três valores de e
Resolvendo na ordem as equações, temos que
A média desses valores é
Passo 3
As energias de banda podem finalmente ser calculadas como:
Então a nossa energia de ionização é o nosso último valor de energia de banda, certo? Porém lembre-se de trocar o sinal!!!!