Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 8.1 - Ex. 79
Suponha que você criou dois pequenos sistemas contendo três átomos cada e que cada átomo pode aceitar energia em quanta da mesma magnitude. (a) Quantos arranjos diferentes existem de dois quanta de energia distribuídos pelos três átomos em um desses sistemas? (b) Você agora junta os dois sistemas. Quantos arranjos diferentes existem se os dois quanta de energia estão distribuídos pelos seis átomos? (c) Em que direção os quanta de energia fluem a partir do arranjo inicial?
Passo 1
O exercício requer do discente a utilização da equação de Boltzmann para descobrir a energia distribuída em cada sistema. Incialmente o discente pode imaginar dois frascos separadamente, cada um contendo três elementos cada em seu interior, tal imaginação deve facilitar o entendimento da questão.
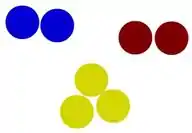
Passo 2
- Primeiramente analisemos que, cada sistema apresenta três elementos, o elemento A (azul), o elemento B (amarelo) e o elemento C (vermelho), em termos de combinações possíveis, temos: A+B, B+C, A+C;
- Posteriormente utilizamos a equação de Boltzmann para determinar a entropia total do sistema, que neste contexto avalia a quantidade de energia desse arranjo de átomos;
- A constante de Boltzmann é 1,38 x 1023 JK-1, W é o número de arranjos em cada sistema e S a entropia total;
- Após realizado os cálculos o mesmo deve ser aplicado ao outro sistema, considerando já nesse contexto 6 elementos dentro do sistema, dada a união dos dois sistemas existentes. Essa união provocará 15 combinações distintas;
Passo 3
- Para o primeiro caso temos, 3 arranjos :
- Para o segundo caso, 15 arranjos
Resposta
- W = 3
- W = 15
- A fluidez energética sempre ocorre espontaneamente, do corpo mais energético para o menos energético, desta forma a fluidez se dará do sistema que possui maior número de quantas para o de menor quantidade, no caso zero.