Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 4.1 - Ex. 93

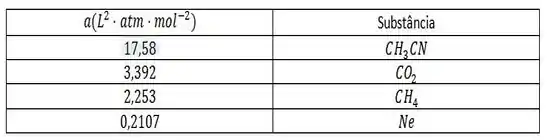
93. A tabela a seguir lista os valores de de , , e . Use seu conhecimento dos fatores que governam as magnitudes de , para atribuir a cada um desses quatro gases um valor de :

Passo 1

Bom!! O parâmetro representa o papel das atrações, e é relativamente grande para moléculas que se atraem fortemente. E qual dentre essas moléculas tem a maior força de atração? Ou melhor!! Qual tem a ligação mais forte?

Humm! Tá na cara que é a molécula de , né não!? Podemos ver isso pelo simples fato de que essa molécula tem uma ligação de hidrogênio presente na sua estrutura, advinda do .

Seguindo a ordem descrescente da nossa lista, temos a molécula de e a moléculas de . Ambas são moléculas apolares que apresentam uma interação molecular do tipo dipolo induzido. Entretanto como o oxigênio é mais eletronegativo que o ; o dióxido de carbono vai ter um maior. Por último, só resta o ; que é um gás nobre, estável e pouco reativo.

Montamos então a seguinte tabela:

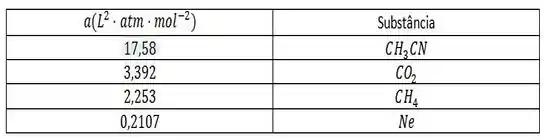
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dando que μ C p = T ( d V / d T ) p - V , deduza uma expressão de μ em termos dos parâmetros de van der Waals a e b e exprima o resultado em termos das variáveis reduzidas. Estime μ a 25°C a 1,0 atm q

A equação termodinâmica de estado ( d U / d V ) T = T ( d p / d T ) v - p foi mencionada neste capítulo. Deduza, a partir dela, a equação seguinte, que é semelhante à anterior: ( d H / d p ) T = - T d

Mostre que para um gás de van der Waals, C p m - C v m = λ R1 λ = 1 -( 3 V r - 1 ) 2 4 V r 3 T r E estime a diferença para o xenônio a 25°C e 10,0 atm.

A relação entre a velocidade do som, C s , num gás de massa molar M e a razão entre as capacidades caloríficas γ , é dada por c s = ( γ R T / M ) 1 / 2 mostre que c s = ( γ p / p ) 1 / 2 , onde p é a

Um gás tem a equação de estado V m = R T p + a T 2 e a sua capacidade calorífica molar a pressão constante é dada por C p m = A + B T + C p , onde a, A, B e C são constantes independentes de T e de p.