Radiação Nuclear
Teoria
Os isótopos nucleares tem váaaaaaaaarias aplicações, que vão desde a medicina até a produção de energia, né? Nesse capítulo a gente vai ver alguns detalhes sobre a radiação, como ela é útil em alguns casos e como, apesar de útil, nem tudo são flores nessa história!
Poder relativo de penetração da radiação ionizante
Apesar de muito boa por diversos motivos, a radiação nuclear pode ser extremamente perigosa para a nossa saúde! Isso porque um certo tipo de radiação, chamada radiação ionizante, possui energia suficiente para ejetar elétrons dos átomos, o que resulta em sérias consequências nos processos biológicos (e é extremamente ligado ao desenvolvimento de câncer).
As radiações alfa, beta e gama, por exemplo, são ionizantes, e o dano na saúde quando somos expostos à elas depende de muitos fatores, como a intensidade da fonte, do tipo de radiação e do tempo de exposição.
A radiação consegue penetrar nosso corpo de maneira inversamente proporcional à sua massa, isso é: quanto mais pesada a partícula, menor vai ser seu poder relativo de penetração.
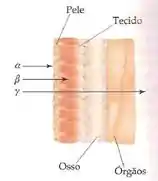
Se liga nessa tabela:
Ou seja, a partícula alfa, que é a mais pesada, é a que menos tem capacidade de penetrar no nosso corpo – ela é embarreirada pela pele. Já a radiação gama, que não tem massa nem carga, é a mais perigosa – você precisa de um metal bem espesso para que ela não atravesse tudo que vê pela frente (prédios, carros, pessoas etc).
Dose absorvida X Dose equivalente
A dose absorvida de radiação é a energia depositada em um sistema exposto à radiação. Por exemplo, se você fica na presença de um isótopo radioativo, a radiação que ele emite vai ser a dose absorvida e você vai ser o sistema! 😊
A unidade usada para medir a dose absorvida é o gray (Gy), que corresponde a um depósito de energia de . Você também pode encontrar a unidade rad (dose de radiação absorvida), que corresponde a Gy.
Maaas, como a gente já viu, não é porque um isótopo emite 10g de partículas alfa que meu corpo vai assimilar essas 10g, né? Isso depende do tipo de radiação! A gente leva em conta então a eficiência biológica relativa, Q, uma constante que relaciona a dose absorvida e a dose equivalente.
Onde a dose equivalente vai ser o tanto que a gente realmente absorve de radiação, já que ela leva em conta o tipo de tecido e o tipo de radiação!
A unidade da dose equivalente no SI é o Sv (sievert), mas antigamente era o roentgen equivalente homem (rem), onde, então não se assusta se você também achar essa unidade.
A eficiência biológica relativa, Q, tem valores fixos pras radiações mais conhecidas e, infelizmente, a gente tem que decorá-los! Para partículas gama, beta e a maior parte das outras radiações, . Para partículas alfa e nêutrons rápidos, .
Mesmo sem trabalhar em uma usina nuclear ou ter que lidar com elementos radioativos, a gente recebe radiação naturalmente de diversas formas e fontes, como nosso prórprio corpo, os raios cósmicos ou diagnósticos médicos.
Essa radiação se chama radiação de fundo, e é a média anual típica de dose equivalente que a gente recebe de fontes naturais. Ela vale cerca de 2 mSV/ano, mas varia de acordo com os nossos hábitos e onde moramos.
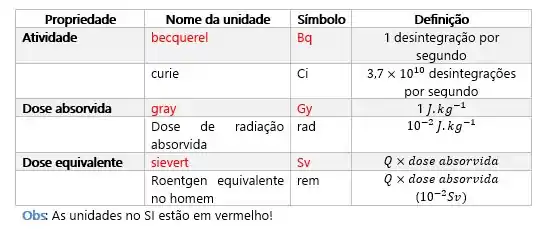
Pequeno resuminho das medidas de radiação 😊
Uso dos radioisótopos na medicina
Os diagnósticos médicos usam muiiiito a radiação e os radioisótopos, principalmente na aquisição de imagens.
Um exemplo bem importante é a tomografia por emissão de pósitrons (o PET), onde a gente ingere um radioisótopo emissor de pósitrons que tenha a ver com o que a gente quer diagnosticar e depois é monitorado. Esse emissor de pósitrons vai participar das funções biológicas normalemente, como se fosse o isótopo não radioativo. A diferença é que, por emitir radiação, o funcionamento do organismo vai poder ser quantificado e analisado por um sensor! Se liga nesse exemplo:
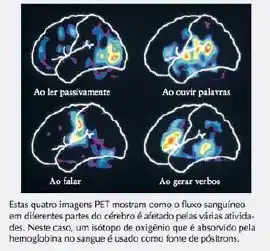
Além do PET e outras técnicas de imagem, a gente pode usar traçadores radioativos. Eles servem para marcar algum átomo importante, que participe das funções biológicas. Por exemplo: a gente pode usar o carbono-14 para marcar a glicose, e conseguir acompanhar a digestão de glicose no organismo.
Como o isótopo radioativo emite radiação que pode ser detectada por sensores, diferentemente dos isótopos não-radioativos, a gente consegue acompanhar o que acontece no organismo com essa molécula marcada! Por isso a gente chama de traçadores radioativos – a gente acompanha o caminho da molécula no metabolismo!
Um exemplo é quando a gente quer descobrir a origem de um átomo numa reação química. Na fotossíntese, por exemplo, se a gente quer saber de onde vem o oxigênio do gás oxigênio liberado, a gente pode fornecer para a planta água marcada com o radioisótopo do oxigênio:
Daí a gente consegue descobrir que o gás oxigênio vem do oxigênio da água, e não do oxigênio do gás carbônico! 😊
Se você tá confuso e pensando que não faz medicina, então não precisa saber de nada disso, relaxa ahahah Vamos fazer uns exercícios que vão te ajudar a fixar e entender mais isso tudo! 😊
Dose absorvida X Dose equivalente
Uso dos radioisótopos na medicina
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.31
Uma amostra de 2 kg absorve uma energia de 1.5 J como resultado da exposição à radiação beta. Calcule a dose em rads e a dose equivalente em sieverts.
Passo 1
A dose em rads é a dose absorvida! A gente sabe que 1 gray (Gy) é 1 J por kg de amostra, e um rad corresponde a Gy.
Ou seja,
No caso do problema, a gente tem 1.5 J por 2 kg:
Passo 2
Para calcular essa dose em sieverts, a gente precisa usar a eficiência biológica relativa, Q, e a fórmula:
Como estamos falando de partículas beta, vamos considerar !
E, então:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Adaptado de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.33
Alguém é exposto a uma fonte de radiação alfa na dose de 1 rad/dia. Sabendo que a náusea começa após uma dose equivalente de aproximadamente 100 rem, após que período esse sintoma da doença da radiação deve aparecer?
Passo 1
Ó, vamos com calma! A gente sabe que a pessoa vai ter uma dose absorvida diária de .
Se a dose equivalente que começa a dar problema é em 100 rem, precisamos usar a fórmula:
Para descobrir a partir de que ponto a dose absorvida se torna problemática!
Como a radiação é alfa, .
Passo 2
Se por dia, a pessoa é exposta à
Assim, vai demorar 5 dias para que a pessoa comece a sentir náuseas.
Resposta
5 dias.
Exercício Resolvido #3
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.51
Explique como você usaria radioativo (um emissor beta com ) para determinar a extensão na qual coelhos são capazes de converter determinado composto de ferro em suas dietas em hemoglobina do sangue, que contém átomos de ferro.
Passo 1
O ferro-59 pode ser utilizado como um traçador radioativo. Ele pode ser incorporado ao componente da dieta que contém ferro e fornecido como alimento aos coelhos.
Depois, é só a gente coletar o sangue dos coelhos e analisar os glóbulos vermelhos. Se o ferro desse alimento tiver sido usado para produzir hemoglobina, os glóbulos vermelhos vão conter o ferro radioativo e vão emitir radiação beta 😊
A porcentagem de hemoglobinas radioativas e não radioativas vai determinar a extensão da utilização desse alimento. Além disso, podemos coletar o sangue em tempos diferentes, para calcular a velocidade de ingestão do ferro, a velocidade de perda do ferro pelo sangue e etc.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.53
Um químico está estudando o mecanismo da seguinte reação da hidrólise de um éster orgânico, o acetato de metila:
A questão é se o átomo de Oxigênio presente no metanol produzido vem do acetato de metila inicial ou da água adicionada. Proponha um experimento que use isótopos e permita determinar a origem do átomo de oxigênio.
Passo 1
Uma solução para isso é utilizar a água marcada radioativamente, com a ajuda de um traçador radioativo, como o . Se a gente usa a , em vez da água normal, conseguimos ver se o metanol incorporou o ou o proveniente do acetato de metila).
Um jeito de ver se o metanol incorporou o oxigênio-18 é calcular a massa molar do metanol. Se ele tiver incorporado, será 34 g/mol, e não 32 g/mol (já que o isótopo radioativo do oxigênio é mais pesado).
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.61
Um rato de laboratório é exposto a uma fonte de radiação alfa cuja atividade é 8,7 mCi.
a) Qual é a atividade da radiação em desintegrações por segundo? E em bequerels?
b) O rato tem massa de 250g e é exposto à radiação por 2 segundos, absorvendo 65% das partículas alfa emitidas, cada uma tendo uma energia de . Calcule a dose absorvida em milirads e grays.
c) Se EBR da radiação é 9,5, calcule a dose efetiva absorvida em mrem e Sv.
Passo 1
a) 8,7 mCi é a atividade na unidade miliCurie! Então, só precisamos fazer uma troca de unidades...
Como 1 bequerel vale 1 desintegração por segundo, podemos escrever que essa radiação tem atividade de
Passo 2
b) Se ele é exposto à radiação por 2 segundos, e a atividade dessa amostra radioativa é desintegrações por segundo, isso quer dizer que ele será exposto à desintegrações!
Se cada desintegração tema energia total que será emitida é:
Se o ratinho absorve 65% das partículas, absorve só 65% da energia!
Passo 3
Agora, precisamos calcular essa energia/massa em grays 😊
Como ,
Passo 4
c) A relação entre a dose absorvida e a dose equivalente é dada pela equação:
Como a gente já sabe a dose absorvida e o enunciado diz que Q=9,5...
Como
Resposta
a)
b)
c)
Exercício Resolvido #6
Lista de exercícios UFPB – Prof Ary da Silva Maia
Uma pessoa de 65 kg é exposta acidentalmente por 116s a uma fonte de radiação beta de 21 mCi proveniente de uma amostra de
a) Qual é a atividade da fonte de radiação em desintegrações por segundo?
b) Cada partícula beta tem energia de e 6,5% da radiação é absorvida pela pessoa. Supondo que a radiação absorvida é espalhada por todo o corpo da pessoa, calcule a dose absorvida em rads e grays.
c) Se EBR das partículas beta é 1, qual é a dose efetiva em mrem e sieverts?
d) Com base na figura abaixo, como a ordem de grandeza dessa dose de radiação se compara com a radiação média de fundo?
Passo 1
a) Nessa primeira etapa, precisamos fazer uma mudança de unidades entre a unidade Curie (Ci) e desintegrações por segundo (ou Bequerel):
Passo 2
b) Se a atividade é de , ou desintegrações por segundo, e a pessoa foi exposta a 116 s de radiação, ela vai ser exposta, no total, à:
Já que a energia de cada desintegração é a energia total produzida por essa emissão vai ser:
A pessoa só absorve 6,5% disso...
Passo 3
Agora, passando isso para grays (J/kg)...
Como ,
Passo 4
c) A dose equivalente e a dose absorvida se relacionam por:
Como Q=1 (o enunciado diz), então a quantidade de dose equivalente em Sv e de dose absorvida em Gy vai ser igual, e a mesma coisa para rem e rad!
Passo 5
d) Essa exposição corresponde a 0,78 mrem, uma radiação muiiiiito pequena se a gente considerar a radiação média de fundo!
Resposta
a)
b)
c)
d) Essa radiação é muito pequena comparada à radiação média de fundo.
Exercício Resolvido #7
Elaboração Própria.
Relacione as radiações naturais alfa, beta e gama com suas respectivas características:
- alfa (;
- beta (;
- gama (;
- Possuem alto poder de penetração, podendo causar danos irreparáveis ao ser humano;
- São partículas leves, com carga elétrica negativa e massa desprezível;
- São radiações eletromagnéticas semelhantes aos raios X, não possuem carga elétrica nem massa;
- São partículas pesadas de carga elétrica positiva que, ao incidirem sobre o corpo humano, causam apenas queimaduras leves.
A sequência correta, de cima para baixo, é:
a) alfa , beta , gama , alfa.b) beta, alfa, beta, gama.
c) alfa, gama, alfa, beta.
d) gama, beta, gama, alfa.
Passo 1
Primeiro, relembrar características de cada radiação:
Alfa ( Pesada, pouca capacidade de penetração. A pele é suficiente para barrear.
Beta ( Leve, capacidade de penetração intermediária. Uma folha de alumínio é suficiente para barrear.
Gama ( Leve, alta capacidade de penetração. Para barrear, é necessário uma grande quantidade de chumbo ou concreto.
Passo 2
Agora que já sabemos as características de cada, vamos resolver o exercício:
a) Possuem alto poder de penetração, podendo causar danos irreparáveis ao ser humano.
A sentença caracteriza uma radiação gama.
b) São partículas leves, com carga elétrica negativa e massa desprezível.
A sentença caracteriza uma radiação beta.
c) São radiações eletromagnéticas semelhantes aos raios X, não possuem carga elétrica nem massa.
A sentença caracteriza uma radiação gama.
d) São partículas pesadas de carga elétrica positiva que, ao incidirem sobre o corpo humano, causam apenas queimaduras leves.
A sentença caracteriza uma radiação alfa.
Resposta
d) gama, beta, gama, alfa.
Exercício Resolvido #8
Elaboração Própria.
Ao acessar um site na internet à procura de informações sobre radiações, um aluno encontrou a seguinte figura:
Qual das radiações é a mais energética e como ela é chamada?
a) É a representada em III. Radiação alfa.b) É a representada em I. Radiação gama.
c) É a representada em II. Radiação beta.
d) É a representada em III. Radiação gama.
Passo 1
Vamos relembrar características de cada radiação:
Alfa ( Pesada, pouca capacidade de penetração. A pele é suficiente para barrear.
Beta ( Leve, capacidade de penetração intermediária. Uma chapa de metal é suficiente para barrear.
Gama ( Leve, alta capacidade de penetração. Para barrear, é necessário uma grande quantidade de chumbo ou concreto.
Analisando a imagem, podemos concluir que a mais energética é a que apresenta maior capacidade de penetração, ou seja, a gama. O que seria a radiação III da figura.
Resposta
d) É a representada em III. Radiação gama.