Velocidade de decaimento radioativo
Teoria
Eaeeee, tudo bom?
A gente sabe que alguns elementos emitem partículas radioativas naturalmente, né?
O interessante disso é que cada um sofre decaimento de uma maneira diferente! Isso é: o urânio-238 demora um tempo para emitir radiação, enquanto o carbono-14 demora uma outra quantidade de tempo.
Mas como a gente mede esse tempo de decaimento?
Lei do decaimento radioativo
A cinética de decaimento de um radioisótopo pode ser medida por uma equação de velocidade de ordem. Ou seja, a gente pode medir o decaimento radioativo de um elemento por:
Onde é a constante de decaimento e N é o número de núcleos restantes após um tempo , e sua expressão é:
Onde é o número de núcleos radioativos inicialmente presentes na amostra.
Como toda lei de velocidade de primeira ordem, o gráfico concentração x tempo é uma exponencial. Mas, no caso das reações nucleares, a gente não mede por concentração, e sim por número de núcleos 😊
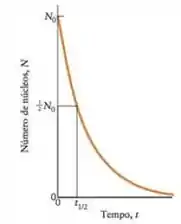
Obs: a velocidade de decaimento nuclear é chamada de atividade, e é expressa como o número de desintegrações por unidade de tempo! A unidade do SI para a atividade é o bequerel (Bq), definido como desintegração por segundo. Além dela, tem uma unidade mais antiga chamada curie (Ci), definida como desintegrações por segundo, velocidade de decaimento de 1g de rádio.
Meia-vida dos elementos radioativos
A meia-vida é uma constante presente em todas as equações cinéticas de ordem. Você lembra que lá nas equações químicas, ela representava o tempo necessário para que a concentração de uma substância caísse a metade, não é?
Nas reações nucleares não vai ser muito diferente!
A meia-vida de um elemento radioativo é o tempo necessário para que se desintegre a metade do número inicial de núcleos!
Por exemplo, o tem meia vida de 28,8 anos. Ele decai segundo a equação:
Isso quer dizer que, se eu começo com 10g de hoje, daqui a 28,8 anos 5g dele já vai ter decaído, liberado os elétrons e se transformado em ítrio-90 (). Se se passarem mais 28,8 anos, os 5g radioativos que eu tinha vão se transformar em 2,5g de estrôncio-90 e 2,5g de ítrio-90, e assim por diante!
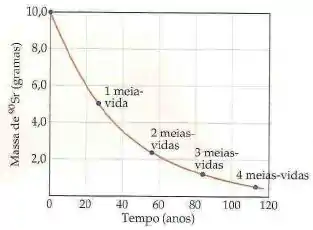
Tem algumas características importantes da meia-vida pra guardar no seu coração:
- Cada elemento tem a sua própria meia vida, que vai de milhares de anos a milionésimos de segundo. Isso depende da identidade do elemento e nada mais 😊
- As meias-vidas não são afetadas por temperatura, pressão ou estado de combinação química. Isso quer dizer que não temos como acelerar a velocidade de decaimento espontânea de um elemento radioativo!
E como a gente calcula esse tempo de meia-vida, numericamente?
Como a meia vida é a medida do tempo necessário para que metade dos núcleos se desintegre, se usarmos na fórmula da velocidade, chegamos a:
Datação por carbono-14
A datação por carbono-14 é uma aplicação importante desse conceito de meia-vida, que serve principalmente para determinar a idade de artefatos arqueológicos através de cálculos pelo decaimento do carbono-14.
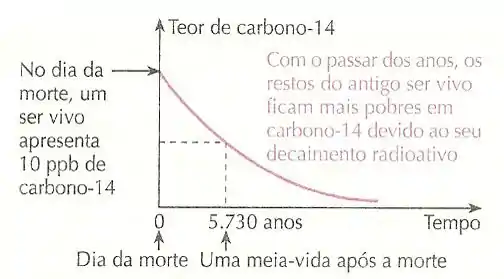
Isso porque o carbono-14 tem o tempo de meia-vida de 5730 anos! Esse isótopo do carbono, embora não seja o isótopo principal, está presente na atmosfera em proporção constante com o Assim, ele participa dos processos biológicos normalmente e tem também uma proporção constante nos organismos vivos (que é cerca de para 1 ).
Quando o organismo morre, os processos biológicos acabam e a quantidade de carbono segue constante, a não ser pelo decaimento do carbono-14! Analisando uma amostra de tecido morto, podemos saber a quantidade de carbono-12 nesse tecido e o quanto deveria ter de carbono-14 (se o tecido tivesse vivo, a partir da proporção fixa).
Assim, fazendo o cálculo com a meia-vida do , a quantidade de carbono-14 que tem no momento da análise e a quantidade que deveria ter se o tecido estivesse vivo, conseguimos calcular o tempo decorrido desde a morte!
Vamos praticar pra fixar tudo isso? 😊
Meia-vida dos elementos radioativos
Datação por carbono-14
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exemplo 17.3
Uma das razões pelas quais as armas termonucleares tem de sofrer manutenção regular é que o trício nelas contido sofre decaimento nuclear. Suponha que uma amostra de trício de massa 1g foi armazenada. Que massa desse isótopo permanecerá após 5 a (1 a = 1 ano)?
A constante de decaimento do trício é 0,0564 .
Passo 1
Para calcular a massa que resta, precisamos usar a lei do decaimento nuclear!
Embora a fórmula seja em número de partículas, a gente também pode usar ela em mols ou em massa! Isso porque o número de partículas é o número de mols vezes o número de avogrado, né? E o número de mols é a massa dividida pela massa molar!
Ou seja: todos esses valores estão interligados, e toda operação matemática que a gente faz na equação (para mudar a unidade de N) também muda a unidade de ! No final, o importante é lembrar que os dois ( só tem que ter a mesma unidade!
Passo 2
Vamos lá então:
Resposta
0,754 g
Exercício Resolvido #2
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.27
Produtos químicos prejudiciais geralmente são destruídos por tratamento químico. Um ácido, por exemplo, pode ser neutralizado por uma base. Por que o tratamento químico não pode ser usado para destruir os produtos radioativos produzidos em um reator nuclear?
Passo 1
Os produtos radioativos produzidos em um reator – que em sequência viram lixo radioativo – vão seguir sua meia-vida e sofrer decaimento natural independente dos processos químicos que a gente faça com eles.
As variações de energia de uma reação química não são suficientes para alterar as propriedades dos núcleos radioativos, tanto que se a gente produzir glicose com carbono-14, por exemplo, essa glicose pode ser queimada a gás carbono que esse gás carbono vai ser o .
Os núcleos vão continuar emitindo radiação e não tem como acelerar a meia-vida deles através de processos químicos ou físicos!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Lista de exercícios UFPB – Prof Ary da Silva Maia
O rubídio-87 é um isótopo natural do rubídio. Se sua constante de desintegração é . Qual a sua meia vida em anos?
Passo 1
Vamos usar a equação da meia-vida!
Como k, a constante de desintegração, vale :
Passo 2
Só passar esse tempo de meia-vida de segundos para anos...
Resposta
Exercício Resolvido #4
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.29
A meia-vida do trítio (hidrogênio-3) é 12,3 anos. Se 48 mg de trítio for liberada de uma usina de energia nucler durante o curso de um acidente, qual massa desse nuclídeo permanecerá após 12,3 anos? E após 49,2 anos?
Passo 1
Ok, vamos lembrar da definição de meia-vida!
A meia-vida é o tempo necessário para que uma amostra radioativa se desintegre pela metade! Isso é, se eu tinha uma massa de 1g, depois de uma meia vida terei 0,5g ainda intacta e 0,5g que já sofreram decaimento radioativo!
Então, se a meia-vida do trítio é 12,3 anos, isso quer dizer que a cada 12,3 anos sua massa cai pela metade!
Se no começo tínhamos 48 mg, depois de 12,3 anos teremos 24 mg!
Passo 2
Vamos continuar descrevendo o decaimento?
Achamos então que daqui a 49,2 anos teremos 3 mg de trítio!
Mas um outro jeito de fazer é simplesmente dividir o número de anos que você quer saber pela meia vida!
Logo, a amostra vai passar por 4 meias-vidas, o que quer dizer que sua amostra vai se dividir por 2 quatro vezes consecutivas!
Atenção: presta atenção porque a amostra não vai ter sua massa dividida por 4, e sim por (porque vai ser dividida por 2, e o resultado por 2, e por 2 de novo e assim vai!)
Resposta
Teremos ainda 24 mg depois de 12,3 anos e 3 mg depois de 49,2 anos.
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.30
Leva 5,2 minutos para uma amostra de 1g de decair para 0,25 g. Qual a meia vida do ?
Passo 1
Vamos ver o que acontece com 1g de passando por suas meias-vidas:
Isso quer dizer que, para chegar a 0,25g o composto precisa passar por 2 meias-vidas.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 14.47
A desoxiglicose marcada com flúor-18 é comumente usada em varreduras PET para localização de tumores. O flúor-18 tem a meia-vida de 109 min. Quanto tempo leva para que o nível do flúor no corpo caia a 10% do valor inicial?
Passo 1
Vambora usar o esqueminha de meia-vida! Se a amostra inicial corresponde a 100%...
Como não temos o valor exato para decair a 10% fazendo o esqueminha, vamos apelar para as fórmulas!
É bom analisar que a gente tem que achar alguma coisa um pouco menor do que 4 meias-vidas (436 min)!
A lei do decaimento diz que:
Se , chegamos a 10% da amostra inicial:
O problema não dá a constante de decaimento pra gente, mas dá uma informação que nos ajuda a descobrir qual que é essa constante: o valor da meia-vida!
Passo 2
Como a fórmula para a meia-vida é:
Substituindo o valor que temos:
Assim, voltando para o que achamos antes...
Resposta
362 minutos
Exercício Resolvido #7
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.35
O rádio-226, que sofre decaimento alfa, tem uma meia-vida de 1600 anos.
a) Quantas partículas alfa são emitidas em 1 min por uma amostra de 5 mg de
b) Qual é a atividade da amostra em mCi?
Passo 1
a) Vamos começar escrevendo a equação de decaimento!
Ou seja, cada núcleo de rádio-226 emite uma partícula alfa!
Para saber quantas partículas alfa são emitidas em 1 min, precisamos calcular quanto de rádio-226 sofre decaimento por minuto, certo?
Na real, então, a gente tem que calcular a velocidade de decaimento por minuto!
Como não temos a constante de decaimento, vamos usar a meia-vida para calculá-la!
Passo 2
Agora que temos k, podemos calcular a quantidade de rádio que decai em 1 min!
Ou seja, de rádio-226 decaem por minuto 😊
A massa de um átomo de rádio-226 é 226u, o que significa que a massa molar desse elemento é 226g!
Em temos:
Como cada átomo emite uma partícula alfa, em 1 minuto os átomos de rádio vão emitir partículas alfa!
Passo 3
b) A definição de Ci (Curie) é desintegrações por segundo.
Nesse caso, a gente tem desintegrações por minuto! Então vamos passar para segundos 😊
Agora, passando para Ci...
Assim, a atividade em mCi () é 4,865 mCi.
Resposta
a)partículas alfa
b) 4,865 mCi
Exercício Resolvido #8
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.41
O potássio-40, que se presume existir desde a formação da Terra, é usado para a datação de minerais. Se existem três quintos do potássio-40 original em uma rocha, quantos anos tem a rocha?
Dados: meia vida do potássio-40 é de .
Passo 1
Para a gente descobrir a idade da rocha, vamos precisar usar a expressão que relaciona a quantidade inicial e a final com o tempo passado:
Como N é de , vamos usar esse dado na fórmula:
Para descobrir t, então, só precisamos calcular o valor de k! E pra isso vamos usar a fórmula da meia vida 😊
Passo 2
Substituindo k na expressão de antes....
A gente pode pensar que o resultado parece certo, já que ele tá próximo da meia vida do potássio-40, mas ainda não chegou ela (e por isso a gente ainda tem mais da metade do elemento na rocha 😊).
Resposta
Exercício Resolvido #9
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.39
A meia-vida para o processo é . Uma amostra de mineral contém 50 mg de e 14 mg de . Qual é a idade do mineral?
Passo 1
Ok, vamos lá! Para a gente calcular a idade desse mineral, precisamos usar tanto o conceito de meia-vida, quanto a velocidade de decaimento!
Se a gente tem 50 mg de urânio-238 e 14 mg de chumbo-206, isso quer dizer que os 14 mg de chumbo vieram do decaimento do urânio!
Assim, a gente pode considerar que a amostra inicial tinha:
Aplicando na fórmula de N...
Como a gente não tem o k, vamos ter que usar a fórmula da meia vida para calcular!
Passo 2
Assim...
Resposta
Exercício Resolvido #10
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.75
Descobriu-se que mols de átomos de radônio-222 ( entraram num porão fechado cujo volume era
a) Qual é a atividade inicial do radônio em picocuries por litro? ()
b) Quantos átomos de permacerão após um dia (24 horas)?
c) Quanto tempo levará para o radnio se decompor a um nível inferior ao recomendado pela Agência de Proteção Ambiental, que é de 4 ?
Passo 1
a) Para calcular a velocidade, precisamos lembrar só da fórmula:
N é a quantidade de átomos envolvidas no processo de decaimento, e isso o enunciado dá pra gente! Para calcular k, vamos usar a meia vida:
A velocidade, então, vai ser:
A atividade em curie (Ci) é calculada por desintegrações por segundo, ou seja, átomos sofrendo decaimento por segundo! Precisamos fazer umas modificações pra chegar em Curie! Vamos lá:
Passando isso para Ci...
Passo 2
Para calcular em Ci por litro, precisamos levar em conta o volume onde os átomos estão!
Como , essa amostra vai ter uma atividade de .
Passo 3
b) Para calcular quanto ainda vai ter no porão, vamos usar a fórmula que relaciona quantidade e tempo:
Passo 4
c) Para se decompor a uma velocidade de 4 pCi/L, ele vai precisar ter essa velocidade de decaimento:
O independe da quantidade de material que tem, ele só depende do elemento! Ou seja, com essa fórmula a gente consegue calcular qual quantidade de radnio vai decair nessa velocidade 😊
O único problema é que as unidades estão todas fora do SI! Para não ter problema, vamos voltar pro SI! Em 1 litro...
Com tudo ajustado, vamos achar N em número de átomos!
Isso em 1 L, né? Mas o porão tem
Ou seja, a partir dessa quantidade a gente vai começar a ter uma velocidade de decaimento de 4 pCi/L. Mas quanto tempo demora pra chegar nessa quantidade?
Resposta
a)
b)
c) 100 dias