Crie um novo modelo. Utilizando os blocos “Sine Wave”, “Mux” e “Scope”, mostre em um mesmo osciloscópio as funções:
Passo 1
O exercício pede para plotarmos três curvas, cujas funções são listadas acima, em um mesmo gráfico.
O modelo deste exercício terá:
- Três entradas, que são as três ondas senoidais dadas pelo enunciado;
- Um bloco “Mux”, que combinará os sinais das três ondas senoidais em um só sinal;
- Uma saída, que será um bloco “Scope”.
Neste exercício, veremos como alterar as propriedades do bloco “Mux”, para que ele tenha três entradas em vez de duas, e teremos que alterar as propriedades dos blocos “Sine Wave”, para criar as ondas senoidais dadas pelo enunciado.
Passo 2
A primeira coisa a fazer é criar as três ondas senoidais, começando por . Em um novo modelo, insira um bloco “Sine Wave”, da biblioteca “Sources”. Para ter acesso às propriedades de “Sine Wave”, clique duas vezes sobre o bloco:

Segundo a própria janela com os parâmetros do bloco, a onda senoidal gerada por “Sine Wave” tem esse formato:
![]()
A onda que queremos criar é , logo a amplitude é , a frequência é , a fase é e o é . Esses são os parâmetros destacados em vermelho acima. Note que não precisamos alterar nada nas propriedades, pois estes são os valores padrão.
Simplesmente feche a janela dos parâmetros e insira um segundo bloco “Sine Wave” ao modelo. Este segundo bloco gerará .
Perceba que ele tem uma fase diferente de , por isso, temos que acessar os parâmetros desse novo bloco que acabamos de inserir e alterar a fase da onda, no campo “Phase (rad)”, destacado abaixo:

Como dito acima, o valor padrão de “Phase (rad)” é , mas a onda tem fase igual a . Portanto, no campo “Phase (rad)”, troque por , como na imagem acima (o SIMULINK entende o como a constante ).
Clique em “OK” para registrar essa mudança. Por enquanto, nosso modelo tem dois blocos:

Passo 3
Vamos inserir um terceiro bloco “Sine Wave” para obter . Também teremos que mexer nas propriedades desse bloco, mas no campo “Frequency (rad/sec)”, destacado abaixo:

O padrão de “Sine Wave” é gerar uma onda senoidal com frequência , mas a onda tem uma frequência de . Portanto, troque no campo “Frequency (rad/sec)” o por, como na imagem acima.
Passo 4
Agora que já temos as três ondas senoidais, vamos inserir o bloco “Mux” para transformar os três sinais em um sinal só e termos as três ondas no mesmo gráfico. Vá à biblioteca “Signal Routing” e arraste o bloco “Mux” para o modelo.

Precisamos aumentar o número de entradas de “Mux”. Dê um duplo-clique sobre o bloco que você acabou de inserir, para ter acesso a suas propriedades:
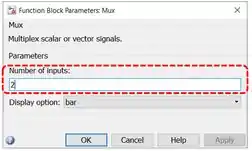
Na janela dos parâmetros de “Mux”, podemos definir o número de entradas do bloco. Altere esse valor para e você verá que aparecerá uma terceira setinha na lateral do bloco:

Conecte cada um dos blocos “Sine Wave” a uma entrada de “Mux”:

Passo 5
Vamos inserir a saída do modelo: um bloco “Scope”. Vá à biblioteca “Sinks”, arraste o bloco “Scope” para o modelo e conecte a saída de “Mux” à entrada de “Scope”:
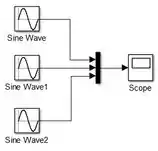
O modelo está pronto. Rode o programa e clique duas vezes sobre o “Scope” para visualizar o gráfico, que terá as três curvas do enunciado.
Resposta
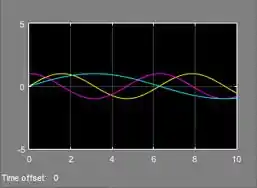
A onda é a curva amarela
A onda é a curva rosa
A onda é a curva azul