No SIMULINK, gere uma onda senoidal de frequência variável (bloco “Chirp Signal”) e a simule por .
- Gere um gráfico do sinal e faça os ajustes necessários para melhorar a resolução do gráfico;
- Utilizando o gráfico, faça uma estimativa da frequência inicial da onda.
Passo 1
Este exercício tem por objetivo praticar a mudança de parâmetros de simulação, como o tempo de simulação, e fazer ajustes no gráfico, de forma que ele fique mais agradável esteticamente. Além disso, vamos praticar a usar a ferramenta para mudar manualmente a escala do eixo horizontal do gráfico: o botão “Zoom X-axis”. Esse botão vai nos ajudar a determinar a frequência inicial da onda senoidal.
O modelo deste exercício terá somente dois blocos: a entrada do modelo será o bloco “Chirp Signal” e a saída do modelo, um bloco “Scope”. Após fazermos a simulação, vamos abrir o gráfico da onda, ver o que precisa ser ajustado e ajustar a escala do eixo horizontal para verificar a frequência inicial.
Passo 2
Vamos começar construindo o modelo de dois blocos. Em um novo modelo, insira um bloco “Chirp Signal”, da biblioteca “Sources”. Não mexa em nenhum parâmetro de “Chirp Signal”, pois o enunciado não especificou os parâmetros da onda senoidal com frequência variável.
Em seguida, insira um bloco “Scope”, e conecte-o a “Chirp Signal”. Dessa forma, o modelo está pronto e tem essa cara:

Antes de executar o programa, ajuste o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por .

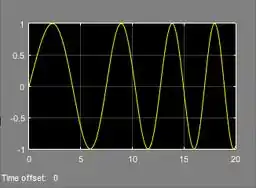
Agora, vamos resolver a letra a do exercício. Rode a simulação e veja como ficou o gráfico. Utilize o botão “Autoscale”, destacado no print abaixo, para a curva se ajustar ao tamanho da janela:
Passo 3
Perceba que a curva não está suave, os vales e as cristas estão “pontiagudos”. Para deixar a curva mais “redondinha”, temos que mudar o tamanho mínimo e máximo do passo do algoritmo da simulação.
Para acessar os parâmetros de simulação, clique sobre a engrenagem da barra superior da janela onde construímos os modelos (destacada em vermelho abaixo):

Aparecerá a janela “Configuration Parameters”. No item “Solver”, encontre os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo), destacados em vermelho abaixo:
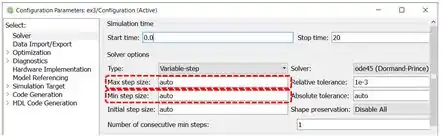
Eles são calculados automaticamente por padrão. Para termos curvs mais arredondadas, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.
![]()
Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo:

A onda não está mais pontiaguda e não tivemos um problema de amnésia. Letra a resolvida =D
Passo 4
Vamos resolver a letra b, que pede para estimar a frequência inicial da onda a partir do gráfico. Para termos a resposta deste exercício, precisamos relembrar alguns elementos básicos de uma onda periódica:
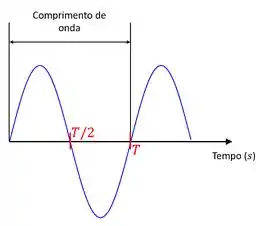
Um dos elementos de um onda periódica é o comprimento de onda, indicado na imagem acima. O comprimento de onda é a medida de um ciclo completo da onda, que pode ser medido entre uma crista e um vale, como indicado acima. Gosto de pensar que é medido considerando um “sobe e desce”
O período é o intervalo de tempo para se completar um ciclo de onda, isto é, o período é medido no intervalo de um comprimento de onda. Falando beeem simplificadamente, é o tempo de um “sobe e desce”. Ele é indicado na figura acima por um vermelho.
A frequência de uma onda é a quantidade de ciclos em um determinado intervalo de tempo. Em uma onda períodica, ela é o inverso do período:
Para estimarmos a frequência inicial da onda senoidal de frequência periódica pelo gráfico, devemos dar um zoom no primeiro “sobe e desce” da onda, no gráfico da janela do “Scope”. Para isto, usaremos o botão “Zoom X-axis”, destacado abaixo:
Clique no “Zoom X-axis” e, em seguida, clique no ponto próximo ao início da curva e arraste. Aparecerá uma linha horizontal, como a da figura abaixo. O comprimento dessa linha horizontal define o grau do zoom que você dará:
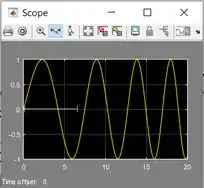
Arraste o ponto final da reta até abranger um “sobe e desce” da onda. O resultado final será mais ou menos assim:
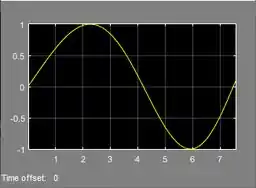
Passo 5
No gráfico acima, note que a crista é mais larga que o vale, indicando que elas têm frequência diferentes. Por isso, vamos usar só a crista para estimar a fequência inicial, considerando que o tempo de duração da crista vale :

Para determinar , vamos uma ferramenta que permite sabermos as coordenadas dos pontos do gráfico. Na barra de ferramentas da janela do “Scope”, onde você acabou de dar um zoom no gráfico, clique em “Try Time Scope”, indicado abaixo:

Perceba que apareceram ferramentas novas. Elas ajudam a analisar o gráfico. Para vermos as coordenadas da curva, clique no botão “Cursor Measurements” com o ícone de uma régua, destacado abaixo:
Aparecerão duas retas verticais no gráfico, com bolinhas onde elas interceptam a curva, e uma janela à direita, indicando as coordenadas dessas bolinhas:

Note que as retas são chamadas de e e na janela à direita, temos as coordenadas de tempo (eixo horizontal do gráfico) e amplitude (eixo vertical) para cada uma delas. Vamos olhar mais de perto a janelinha que dá as coordenadas:
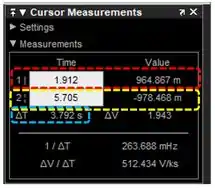
Destacado em vermelho, temos as coordenadas da reta e, em amarelo, da reta .
E, o mais importante para este exercício, em azul, temos a diferença entre as coordenadas de tempo das bolinhas da reta e da reta . Perceba no print acima que a coordenada da bolinha da reta no eixo horizontal é e que a da reta é . Em azul, temos o que é .
É nesse campo que obteremos para calcular a frequência inicial da onda.
Para isto, selecione a reta e arraste-a até o início do gráfico, isto é, até o começo da crista. Em seguida, selecione a reta e arraste-a até o final da crista. Dica: você pode usar as setinhas do teclado para levar as retas mais à direita ou à esquerda.
Sua janela ficará parecida com essa:
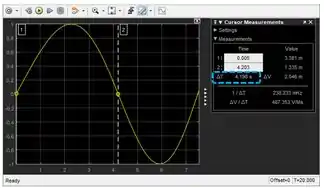
Veja o campo do , destacado em azul acima. O valor dele equivale a , logo, temos que:
Como a frequência é o inverso do período, temos:
Resposta
- Gráfico da onda senoidal de frequência variável:
- A frequência inicial da onda é de aproxidamente .