Resolva pelo método da adição:
Passo 1
A ideia do método da adição é você somar as duas equações, e quando fizer isso uma das incógnitas some (ou é zerada).
Vamos olhar para o nosso sistema:
Perceba que se a gente somar as equações, a nossa variável y vai zerar, por que:
Assim, não precisamos fazer modificações, podemos apenas somar nosso sistema.
Passo 2
Somando:
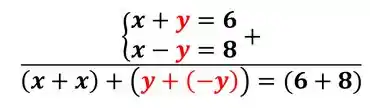
Agora, fazendo essa conta, temos:
Passo 3
Depois de descobrir o valor de uma incógnita, voltamos a uma das primeiras equações e substituímos. Vamos fazer isso na primeira:
Descobrimos que , assim :
Assim, o par ordenado é solução da nossa equação.