Resolva o sistema:
Passo 1
Temos um sistema de três incógnitas, para resolver vamos fazer o escalonamento, que é deixar nosso sistema parecido com uma escada, ou seja, vamos zerar essa parte:
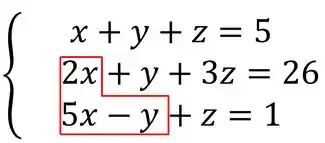
Vamos começar zerando a incógnita x da segunda e terceira equação.
Na segunda equação, temos:
Para zerar o , precisamos de , mas na primeira equação temos apenas . Assim, vamos multiplicar a primeira equação por
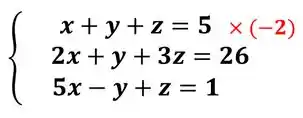
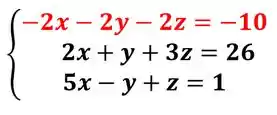
Agora, vamos somar na segunda linha:
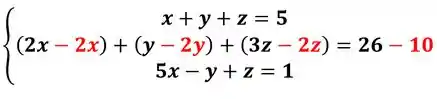
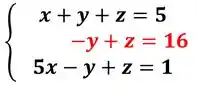
Agora, vamos zerar o da terceira equação, temos:
Precisamos de , para isso vamos multiplicar a primeira equação por -5:
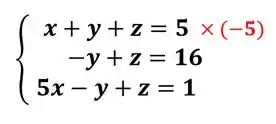
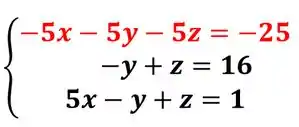
Somando na ultima:
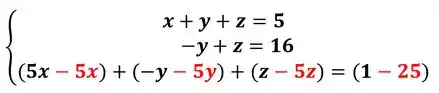
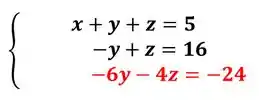
Passo 2
Vamos zerar o y, na ultima equação, temos:
Para fazer isso, precisamos somar , e na segunda equação, temos . Então podemos multiplicar a segunda por .
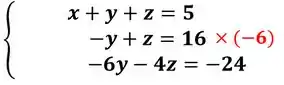
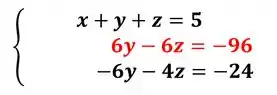
Somando:
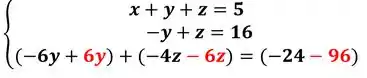
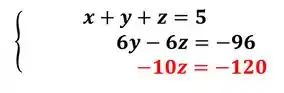
Passo 3
Agora que temos o sistema escalonado, vamos isolar as incógnitas, da ultima equação temos:
Agora vamos para a segunda equação e substituindo o valor de z:
Agora na primeira equação: