Resolva pelo método da substituição:
Passo 1
O método da substituição, nada mais é do que isolar uma das incógnitas e substituir na outra equação. Vamos dar uma olhada no nosso sistema:
Já na primeira equação, temos que o x já está isolado:
Agora é só substituir na segunda equação esse valor de x.
Passo 2
Substituindo:
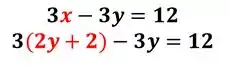
Agora é só resolver essa equaçãozinha :
Passo 3
Agora que descobrimos o valor de y, vamos voltar na primeira equação e substituir
Assim, o par ordenado é solução da nossa equação